Clustered Bodies

If you are looking for a challenge, go no further than the dynamics of clustered spinning bodies. You can go back to Eq. (6.32) and sum over all particles, just as we did for a single body. Executing all of these steps would blow the chapter. Fortunately, we do not have to start from scratch, but take advantage of the angular momentum of clustered bodies, Eqs. (6.24) and (6.25). These equations serve two distinctively different situations. Equation (6.24) represents the more general case of moving bodies, whereas Eq. (6.25) assumes that all bodies c. m. are mutually fixed.

The second case is more important and easier to deal with. It applies to air vehicles with spinning machinery, like turbines, rotors, propellers, or flywheels. I will deal with it first. If your stamina has not been exhausted by then, you may continue with the more general case that applies to rotating and translating objects within the vehicle. Imagine a jeep being pushed backward in a cargo aircraft for parachute drop, or the movement of the space shuttle’s manipulator arm before release of a spinning satellite. I believe, however, both cases would be fun to explore.

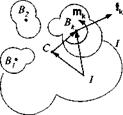
Fig. 6.15 Clustered bodies.

For both cases we begin with Euler’s second law Eq. (6.32) and sum over all particles of rigid body В

E D’lii = Ew’7

І І

which can be abbreviated by

D‘lf = m,

Now consider к rigid bodies Bk, к = 1, 2, 3,… with their external moments mk and forces fk (see Fig. 6.15). Summing over the entire cluster and shifting the reference point of the forces from their individual c. m. Bk to point I

m, = + j2SB*ifk

к к

yields

D‘ E^*7 = + E swfk

к к к

where we abbreviate the left side by D1 J2k ^ = В>Ії^Вк1

DllfBkI = E"1^ + E SBtifh (6-48)

к к

We zero in on the angular momentum of clustered bodies lfBkI using Eq. (6.24) with / as reference point

lTkI = E (іВвУкІ + mBkSвкІD1 sBti)

к

and introduce the common c. m. C of the cluster sbki — sbkc + sci into the last term

= E™SiSBtcDVc + Emg* SciD1Sq

к к к

+ SCi’S^mBkDIsBkc + y^jmBkSBkcDISci

к к

The last two terms vanish because C is the common c. m. Therefore

lfBkI = £/f‘wBt/ + J2mBtS^cD’sBtC + J2mBkSciD’Sa (6-49)

к к к

At this juncture the two cases require separate treatment. For the fixed case D/s, stc can be simplified because DcsBkC = 0. No such reduction is possible for moving bodies.

6.3.4.1 Mass centers are mutually fixed. Let us modify the second term on the right-hand side of Eq. (6.49) by transforming the rotational derivative to the C frame, which consists of the points Bk and the common c. m. C:

SBkc D1 s Звкс{0С s вкс + fiC/$stc)= ^m5tSstcfiC/$stc

к к к

Reversing the vector product and transposing the skew-symmetric displacement vector yields

Y^mBkSBkcQCISBkc = ^2mBkSBkCSBkcUCI

k k

We arrive at an intermediate result if we substitute this expression into Eq. (6.49) and recognize that the first two terms on the right-hand side of Eq. (6.49) are in effect Eq. (6.25):

/?Bi/ = lcBkl + £mB‘SaD/sCj

к

Substituting the angular momentum into Eq. (6.48) and introducing C as a refer­ence point at the right-hand side, we obtain

D‘llBtl + Dl (y^m^SaD^cA = £mB* + £ SBtcfk + $ci £ Л

к /к к к

Applying the chain rule to the second term and combining it with the last term produces a familiar equation

£mB‘Sc/D;DV/ = SaJ^fk = Saf

к к

which represents Newton’s equation applied to the common c. m. It is satisfied identically, and therefore Euler’s equation for bodies with mutually fixed mass centers consists of the remaining terms:

D’ll*1 =Y, m*+Y, SBkCfk

к к

For the final form, most useful for applications, we reintroduce Eq. (6.25):

£ Dl{tBB“Bkl) + £ D‘ (mB*SBtcSBkcua) = £«* + £ SBtCfk (6.50)

к к к к

Given the MOIs of the individual bodies Вk, their displacements, angular rates, and their external moments mk and forces f k, we can model their attitude equation. Let us apply it to an important example.

Example 6.11 Dual-Spin Spacecraft

Problem. A satellite, orbiting the Earth, is subject to perturbations that slowly change its attitude, unless thrusters correct the deviations. Such a control system is expensive to implement. Earlier in the space program, satellites would carry a rapidly spinning wheel that would maintain attitude just by the shear magnitude of its angular momentum.

The satellite consists of a cylindrical main body fi| and a cylindrical rotor B2, with their respective c. m. B and B2 and mass mB’ and mBl. The rotor re­volves about the third axis of the main body with the angular velocity coBlR’ ]Bl = [0 0 R], and the main body’s inertial angular velocity is [®B|/]S| = [p q r]. With the rotor placed at the common c. m., the points B,B2, and C coincide. Both MOIs are referenced to B and given in ]B| coordinates

lf+2 0 0

0 lf+1 0

о 0 lf+2

Derive the scalar differential equations of the satellite, free of external forces and moments.

Solution. Because the centers of mass are mutually fixed, Euler’s law for clustered bodies [Eq. (6.50)] applies:

With loBi> = u>BlB< +tuBl/, point B2 — B, and abbreviating if +IB2 = IB+Bl
D‘(IBB+Вїшв’1 + ІВв]шВіВі) = 0

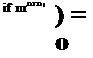Transform the rotational derivative to the frame of the main body B:

The MOI of both the main body and the rotor (cylindrical symmetry) do not change wrt the main body; therefore, their rotational derivatives are zero, and we have arrived at the invariant formulation of the dual-spin spacecraft dynamics:

(6.51)

Let us use the main body’s coordinates ]Bl to express the equation

+[£lB>I]B'[l^]B'[coB2B’]Bl = [0]Bl

Substituting the components and multiplying the matrices yields the scalar differ­ential equations of a dual-spin spacecraft:

It 1+2P + (Iz+1 – IBl+V + IpRq = 0

IBl+2q – (lBwl – Ij’+2)pr – lB2Rp = 0 (6.52)

IB’+2r + IB2R= 0

The rotor’s angular momentum IBlR dominates with its high spin rate R the term (1B’+1 — IBw2)r and provides the stiffness for the satellite’s stabilization.

As a historical note, the first U. S. satellite Explorer I, launched in February of 1958, was spin stabilized but started to tumble after a few orbits. NASA overlooked the known fact that an object with internal energy dissipation is only stable if it is spinning about its major moment of inertia axis.

6.3.4.2 Mass centers are translating. Clustered bodies whose c. m. are translating relative to each other are more difficult to treat because the common c. m. is also shifting. We start with Eq. (6.49). Substituting Eq. (6.49) directly into Eq. (6.48) and introducing SBki = SBkc + Sci into the last term yields

X)Dl (!BBk“Bkl) + X mBk Sb‘c D’ D‘Sb>c + X щВк SaD’ D’Sci

к к к

= X] mBk + X sBtcfk + Sci X /*

к к к

where we expanded the second and third terms by the chain rule and took advantage of the vanishing vector product of like vectors. Embedded in this equation is Newton’s second law premultiplied by Sci-

Y, mB’SaDIDIsa = SciY, fk

к к

These two terms are satisfied identically. Voila, we have arrived at the Euler equa­tion of mutually translating bodies referred to the common c. m C:

X^(/^’) + X-^c^w = X"* + £W* (6.53)

к к к к

where the right-hand side sums up the moments applied to the common c. m. C:

mc = Хтв* + XSb‘c^

к к

The equation of motion consists of the MOIs IlBi of the individual parts and their inertial angular rates шВк’ plus an extra transfer term J2kmBk $BkcD! Drs вкс with a peculiar acceleration expression D1 D! sвкс■ This is the acceleration of the dis­placement vector s Btc as observed from inertial space. It does not include the inertial acceleration of the common c. m. For clarification we introduce the vector triangle Sekc =SBti -sci’-

D1 DfsBkc – D1 DlsBki – D1 D1 sci = aBk – a’c

As it turns out, it is the difference between the inertial accelerations of the individual c. m. Bk and the common c. m. C.

Example 6.12 Carrier Vehicle with Moving Appendage

A main vehicle B carries an appendage Bo, whose c. m. is moving wrt the carrier. Typical examples are the deployment of a satellite from the space shuttle, the swiveling nozzle of a rocket, or the tilting nacelle of the Osprey-type aircraft. In each case the common c. m. C is not fixed in the vehicle. In these applications it would be more convenient if the equations of motions were referred to a fixed point, usually the c. m. of the main body of the aircraft or missile. We can make that switch by transferring Euler’s equations to the c. m. B of the carrier vehicle.

We derive the attitude equations from Eq. (6.53), specialized for two bodies:

(6.54)

To replace C by B, we make use of two relationships, the moment arm balance and the displacement vector triangle,

mBlsBlc + mBlSB2c = 0

$ BiC — Sb2C = —SB2B

Adding both equations, after the second one has been multiplied first by mBl and then by — mB’, yields the two relationships

Substituting these two displacement vectors into the third and fourth terms of Eq. (6.54), and into the last two terms, removes the dependency on the common c. m. C. After two pairs of terms are combined, we have produced Euler’s equation for a carrier vehicle B with moving appendage By.

D'(Ibbojb’1) + D

= mBl +mBl

Do you recognize the two rotary terms, the transfer term that contains the inertial acceleration of the displacement vector, and the external moments and forces? It may be puzzling what the state variables are. We can take two perspectives. For the applications that I mentioned, the translational and angular motions of the appendage are known as a function of time. Therefore, only шв” contributes three body rates as state variables. The differential equations are linear. If, however, the appendage has its own degrees of freedom, like the shifting cargo during aircraft maneuvers, шВг1 and Sb2b, become also state variables. Additional equations must be adjoined to furnish a complete set of differential equations, which will couple the motions of the two bodies. The whole set of equations are nonlinear and, as you can imagine, difficult to solve. To become familiar with the solution process, you should attack Problems 6.14 and 6.15.

6.3.4.3 Summary. With Euler’s law firmly in your grasp, you are fully equipped to model all aspects of aerospace vehicle dynamics. Never mind whether it is derived from Newton’s law or is a principle in its own right. What counts is that you are able to apply it correctly. From first principles I have built Euler’s equation for rigid bodies, either referring it to the c. m. or another fixed point. The free-flight attitude equation uses the c. m. to detach itself from the trajectory parameters, enabling the separation of the translational and attitude degrees of freedom. You should have no problem to derive the full six-DoF equations of motion of an airplane, missile, or spacecraft. The difficulty lies in the modeling of aerodynamics, propulsion, and supporting subsystems. We will pick up this challenge in Part 2.

I also introduced you to the dynamics of clustered bodies. In most aerospace applications their mass centers are fixed among themselves. Under those circum­stances the transfer term includes only one time differentiation. If the bodies are moving, second-order time derivatives of the displacement vectors appear. Partic­ularly important are spinning rotors, which introduce desired (momentum wheels) or undesired (propeller, turbines) gyroscopic effects. Because of their significance, we devote a separate section to their treatment.