Coriolis Transformation

Unequivocally, Newton’s law must be referred to an inertial frame of reference I. Starting with such a frame however, we can use Euler’s transformation of frames and shift the rotational derivatives over to another, noninertial reference frame R. The additional terms are moved to the right side as apparent forces to join the actual forces. Our goal is to write Newton’s second law just like Eq. (5.9), but replace I by the noninertial reference frame R and include the additional terms on the right-hand side as corrections

mB DRVg = f + correction terms

We begin with Newton’s law in the form of Eq. (5.8) and introduce the vector triangle of displacement vectors shown in Fig. 5.7. В is the c. m. of body B, whereas the reference points R and I are any point of their respective frames

вві = SBR + Sri

Substituted into Eq. (5.8)

mBDID, sBR + mBD, D,sRl = f (5.23)

The second term represents the inertial acceleration of the reference frame and needs no further modification. However, both rotational derivatives in the first term must be shifted to the reference frame R. Let us work on this acceleration term alone:

D’D’sbr = D‘(DrSbr + nRIsBR)

= Dr(Drsbr + nR[sBR) + nRI(DRsBR + nR, sBR)

= DrDrsbr + DR(nRIsBR) + nRIDRsBR + nRlnRlsBR = DrDrsBr + 2 flRIDRsm + nRInR, sBR + (DRnRI)sBR

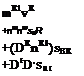Substituting the definition of the relative velocity vR — DrSbr into Eq. (5.23) and moving all terms except the relative acceleration to the right yields the Coriolis form of Newton’s second law:

If the observer stands on a noninertial frame, he can apply Newton’s law as long as he appends the correction terms. There are four additional terms. The first three involve the body, and the last one relates only to the reference frame. The Coriolis acceleration acts normal to the relative velocity vRfi and the centrifugal accelera­tion outward. The angular and linear acceleration terms have no special name and appear only if the reference frame is accelerating.

Example 5.7 Earth as Reference Frame

Earth E is the most important noninertial reference frame for orbital trajectories. It has two characteristics that simplify the Coriolis transformation. Both the angular acceleration is zero, DI0,E’ — 0, and the linear acceleration of Earth’s center E vanishes, D1 D1sri = 0.

Thus, the simplified Coriolis form of Newton’s law emerges from Eq. (5.24):

mBDEvEB = f – mB(2EIeiveb + EIeiEIeisbe) (5.25)

with only the Coriolis and centrifugal forces to be included as apparent forces; sBE is the displacement vector of the vehicle c. m. wrt the center of Earth, vB is the vehicle velocity wrt Earth (geographic velocity), and flEI Earth’s angular velocity.

If you are the passenger in a balloon that hovers over a spot on Earth, you are only subject to the apparent centrifugal force. But when the balloon starts to move with vf, the Coriolis force kicks in. The faster the geographic speed, the greater the force, except if you fly north or south from the equator, then the cross product flEIvB vanishes.

The Coriolis force is responsible for the counterclockwise movement of the air in a hurricane on the northern hemisphere. Newton’s law governs the motions of the air molecules. As the atmospheric pressure drops, the depression draws in the air particles. Those south of the depression are moving north at velocity vB and are deflected by the Coriolis force mB2flEIvB to the east. The northern air mass veers to the west as it is pulled south. These flow distortions set up the counterclockwise circulation of a hurricane.