EQUATIONS OF MOTION FOR A RIGID AIRFRAME

To fully understand the stability characteristics of an aircraft and why certain responses occur, it is necessary to determine the equations governing its motion and to define the parameters that dominate and influence them. The method used in this chapter to develop the necessary equations relies on a number of simplifying assumptions but applies to any rigid body (neglecting any structural distortion) which is subjected to small disturbances. By making such assumptions these essentially non-linear equations can be linearized and the task of analysing them is made much simpler.

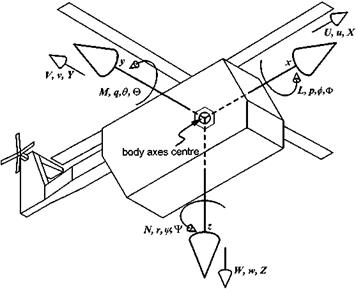
Figure 4.2 shows a set of rectangular axes (O, x, y, z) fixed in the helicopter (body axes) with its origin at the body axes centre. Note that at this level of complexity the rotor dynamics are ignored. The rotor is assumed to be a fixed force and moment generating device. The components of velocity and force along the Ox, Oy and Oz axes are U, V, W and X, Y, Z respectively. The components of the rates of rotation about the same axes are p, q and r and the moments L, M and N. After Babister [4.2], consider an arbitrary point P at position x, y, z from the body axis centre, which has local components of velocity and acceleration u, v, w and ax, ay, az respectively.

The absolute velocity of the point P is now obtained by superimposing the velocity of the body axes centre onto the relative velocity of the point P. P is moving relative to the body axes centre, but this centre is also moving, so the absolute velocity of P is given by the sum of these two components. The body axes centre is moving with velocity U, V, W so denoting the absolute velocity of P by u’, v’, W leads to:

Fig. 4.2 Body axes system.

and similarly, the absolute accelerations are:

a’x = u’ — rV + qw’ dy = V — pW + ru! dz = W — qu’ + pv’ (4.2)

The values of u’, v’, W’ can be obtained by differentiation and since the airframe is rigid, y = x = z = 0:

u’ = І7 — yv + zq v’ = V — zp + xv w’ = W — xq + yp Substituting for u’, V, W and for u’, V, W’, using Equations (4.1) and (4.2), leads to: dx = U — rV + qW — x(q2 + r 2) + y(pq — V) + z(pr + q) 4

dy = rU — V—pW + x(pq + V) — y(p2 + r 2) + z(qr — p) > (4.3)

az =—qU + pV + W + x(pr — q) + y(qr + p) — z(p2 + q2) J

Having obtained expressions for the components of the absolute acceleration of the point P, consideration must now be given to the forces acting on the helicopter. To this end, consider an element of mass Sm at the point P Using the formula F = ma, the forces producing the components of acceleration a’x, dy, dz are dx Sm, dy Sm, dz Sm respectively. The total force is obtained by summing the components of force at all such points over the whole helicopter using Equation (4.3):

X = m{U — rV + qW — dx (q2 + r 2) + dy (pq — V) + dz (pr + q)} 4

Y = m{rU +V—pW + dx (pq + V) — dy (p2 + r 2) + dz (qr — p)} > (4.4)

Z = m{ — qU+pV + W + dx(pr — q) + dy(qr + p) — dz(p2 + q2)} J

where dx, dy, dz are co-ordinates of the centre of gravity from the body axes centre. The forces acting on the particle at point P will each have an associated moment

about the axes. First consider the moments about the Ox axis; these will be rolling moments and will be denoted by L.

The elemental force Sm. a’z has a moment about Ox given by:

moment = (Sm. a’z )y clockwise

The elemental force Sm. a’y has a moment about Ox given by:

moment = (Sm. a’y )z anticlockwise

Since the third elemental force Sm. a’x has no moment about Ox, the total moment for such points is given by:

L = & Sm(a’z y — a’y z)

Hence from Equation (4.2):

l=p&(zi)8m+<f2—Sm+^—q&xym (4.5)

— (pq + r)&xzSm + ( — qU+pV+ W)&ySm — (rU+ V—pW)&zSm )

Moments and products of inertia are defined about the body axes centre as follows:

[Ixx ]b = &( y2 + z 2 )Sm = moment of inertia about x axis [Iyy ]b = &(x 2 + z 2)Sm = moment of inertia about y axis [Izz]b = &(x2 + y2)Sm = moment of inertia about z axis [Iyz ]b = & yz Sm = product of inertia about y and z axes [Ixz ]b = & xz Sm = product of inertia about x and z axes [Ixy ]b = & xy Sm = product of inertia about x and y axes

So equation (4.5) can be rewritten as:

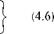L = p [Ixx ]b + qr([izz ]b — [Iyy ]b) + (r 2 — q2 )[iyz ]b + (pr — q)[lxy ]b

— (pq + r)[Ixz ]b + ( — qU+pV + W) &y Sm — (rU + V—pW) &z Sm

Since the body axes centre is not necessarily at the centre of gravity the following transformation is required:

[Ixx ]b = Ixx + m(d 2 + d|)

[Iyy ]b = Iyy + m(d 2 + d 2)

[Izz ]b = Izz + m(d 2 + d 2)

[Ixy ]b = Ixy + mdx dy [Ixz ]b = Ixz + mdx dz [Iyz ]b = Iyz + mdy dz

Therefore Equation (4.6) becomes:

L = pIxx + qr{izz — Iyy} + (r 2 — q2 )Iyz + (pr — q)Ixy — (pr + r)Ixz — Ydz + Щ

By a similar analysis, equations for moments M and N can be determined:

L = ptxx + qr{Izz – Iyy} – (pq + f)Lcz – (q2 – r 2 )Iyz – (q – pr)Ixy – Ydz + Zdy Ї M = qIyy-pr{Ixx – Izz} – (r 2 p2 )Ixz – (r – pq)Iyz – (p + qr)Ixy – Zdx + Xdz (4.7)

N = rIzz + qp{Iyy – Ixx} – (p – qr)Ixz – (q +pr)Iyz – (p2 – q2)Ixy – Xdy + YdxJ where dx, dy, dz are co-ordinates of the centre of gravity from the body axes centre and Ixx, Iyy, Izz, Ixy, Iyz, Ixz are the moments and products of inertia about axes through the centre of gravity parallel to Ox, Oy, Oz. Linearizing the force and moment equations (Equations (4.4) and (4.7)) by means of the small perturbation theory and assuming that the CG is co-incident with the body axes centre leads to:

X = m{u + qWe}

Y = m{v – pWe + rUe}

Z = m{w – qUe}

L = Ixx p – Ixz r M = Iyy q

N = Izz r – Ixz p J

Noting that the forces and moments arise from aerodynamic, gravitational and control sources and introducing the concept of derivatives, Equation (4.8) becomes:

mu = uXu + wXw + q(Xq – mWe) – Qmgcos0e + B1 XBi + 0cX0c

mr = vYv + p(Yp + mWe) + r(Yr – mUe)

+ фmg sin 0e + tymg cos 0e + A1 YAl + 0TR Y, TR

mw = uZu + wZw + q(Zq + mUe) – 0mgsin0e + BAZB| + 0cZ0c

Ixx p – Ixz r = vLv +pLp + rLr + a1 La + 0TR L0TR

Iyy q = uMu + wMw + qMq + Bi MB| + 0c M0c Izzr – Ixzp = v^Vv +pNP + rNr + A! NAl + 0TRT^0TR

These equations are often expressed in matrix form as indicted below in the discussions on dynamic stability and control response (Section 4.11).