Finite Wing Flapping

The finite wing flapping differs, especially for the low aspect ratio wings, from the 2-D oscillatory motions of airfoils because of the presence of the tip vortex which is likely to interact with the leading edge vortex of the wing. For the large aspect ratio wings, however, the strip theory, based on the quasi 2-D approach, can give the approximate values for the total lift and the propulsive force once the type of motion is described. During the flapping of the wing, since the heaving amplitude changes linearly along the span, the dynamic separation angle also changes from one strip to another as well. Therefore, one has to make sure that each strip does not experience the dynamic stall. If there is a dynamic separation present in any strip then the leading edge vortex must be checked for bursting so that it does not lose its suction force. In case of a lost of suction in any strip, the contribution coming from that strip to the lifting and propulsive force must be reduced from the total accordingly (DeLaurier). Based on their modified strip theory Mueller and DeLaurier give their predicted averaged total thrust coefficient as negative and it agrees well with experimental values for a specific wing at low reduced fre­quencies, i. e. k < 0.1, which indicates power reduction, i. e. windmilling. There is an over estimated positive thrust for k > 0.1, and the over estimation is as high as 10%, for the reduced frequency of k = 0.2. The theoretical and the measured lift coefficients remain almost constant with respect to reduced frequency, wherein the theory over estimates the lift coefficient about 15% compared to experimental values.

Further experimental studies were conducted to model the 3-D dynamic stall of low aspect ratio wings oscillating in pitch (Tang and Dowell 1995) and (Birch and Lee 2005). Tang and Dowell modeled a low aspect ratio wing with a NACA 0012 in periodic pitch, and they observed that results of their simple model showed qualitative similarities with the data of corresponding 2-D airfoil. Birch and Lee, on the other hand, investigated the effect of near tip vortex behind the pitching rectangular wing with NACA 0015 airfoil profile having aspect ratio of 2.5 at Re = 1.86 x 105 within the reduce frequency range of 0.09-0.18. Their experi­mental results indicate small hysteretic behavior during the upstroke and down – stroke motions for both the attached and the light stall oscillations. In case of deep stall oscillations, however, during upstroke the lift and the lift induced drag values increased with the airfoil incidence more than during downstroke for which the size of the tip vortex was larger compared to that of upstroke.

More detailed and extended wind tunnel as well as numerical study of oscil­lating finite wings was given by Spentzos et al. Five different wing geometry, varying from rectangular to highly tapered planforms with swept back tips, whose aspect ratios ranging from 3 to 10 and Reynolds numbers ranging from 1.3 x 104 to 6 x 106, are studied in dynamic stall conditions. The reduced frequencies of pitching oscillations range from 0.06 to 0.17. A light stall study of a rectangular wing with NACA 0015 section and with aspect ratio of 10 at Re = 2 x 106 and M = 0.3 indicates that hysteresis curves for the lift and the drag narrow down considerably from half span to the tip both for the experimental and the compu­tational results. At the tip region, however, there is a considerable positive shift between the experimental and the numerical results for the coefficients, which is attributed to the flexibility of the wing at the tip region (Spentzos et al. 2007).

The spanwise flexibility is also effective in thrust production of a pitching plunging finite wing (Zhu 2007). For a flexible wing, modeled as a thin foil in air, there is an initially sharp increase in thrust coefficient with increase in the stiffness of the foil, and it remains almost constant after dropping to a certain stiffness value. However, the efficiency shows a small increase with increasing stiffness. The increase in the average pitching angle decreases the amount of thrust but has an increasing effect on the efficiency of the foil. Nevertheless, for hydrofoils, where the calculations are performed for water, the thrust gradually increases with increasing stiffness, and the efficiency decreases slightly. The effect of average pitching angle is the same as it was for the case of air. The effect of spanwise flexibility on the thrust of a finite wing may change with the tip vortex and the leading edge vortex interaction which may enhance or weaken the leading edge suction force created by the foil. For more precise assessment, further investiga­tions for the wings with tip vortex reducing devices become necessary.

The frequency of the flapping plays additional essential role in finite wing flapping because of presence of the tip vortex. As the frequency of the flapping increases, the vortex generation frequency also increases during the creation of lift. The starting vortex, the tip vortices shed from the left and the right tips of the wing and the bound vortex on the wing itself altogether form a vortex ring during the downstroke. At the end of the downstroke, since there is no lift on the wing, the bond vortex becomes a stopping vortex as shown in Fig. 8.43.

The starting and stopping vortices are equal in magnitude but opposite in sens, and both are normal to the free stream direction. The size of the idealized vortex ring in Fig. 8.43 depends on the wing span and the frequency of the flapping.

Fig. 8.43 Starting and stop­ping vortex generated during the downstroke

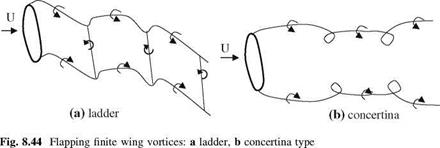
For the case of high frequency flapping the starting vortex can not move down­stream away from the wing, therefore, it affects the lift unfavorably. On the other hand, once the wing is at its lowest position for upstroke, the effective angle of attack must create a lift generating vortex so that another starting vortex, which is in opposite sign with the stopping vortex, forms after a little lag. At the end of the upstroke, when the wing is its top position, a new stopping vortex, which is almost equal to the previously formed stopping vortex, and the new tip vortices are formed to make a new vortex ring. This way, once a cycle of motion is complete with downstroke and upstroke a ladder type wake, which consists of stopping and starting vortices, is generated as shown in Fig. 8.44a.

In the ladder type wake, which is produced by flapping finite rigid wing, the starting vortex having an opposite sign with the bound vortex causes delaying effects on the lift. In order to avoid this delay and not create vortices which are normal to flight direction, the length of span is reduced during upstroke with making use of spanwise flexibility. During downstroke the wing has a full span to give wider gap between the tip vortices whereas this gaps narrows down because of having smaller wing span during upstroke, which makes the strength of the tip vortex to remain the same. Hence, in an alternating manner, we observe one wide and one narrow tip vortex street, which in literature is called concertina type wake as shown in Fig. 8.44b, Lighthill (1990). In concertina type, unlike the ladder type, the periodic occurrence of wake vortices normal to the flight direction which plays a delaying effect in lift generation, disappears. Therefore, the spanwise flexibility, which generates concertina type wake pattern is preferable for man made flapping wings having high aerodynamic efficiencies similar to the efficiencies of the wings exist in nature.