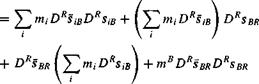Kinetic Energy

You may have heard of the flywheel-car project. Instead of using battery power as alternate energy, the car is driven by the kinetic energy stored in a massive flywheel. You drive up to a filling station, plug the drive motor into an outlet, and spin up the wheel. Supposedly, the stored energy could propel you 50 miles around town. How do we calculate the stored energy of a flywheel and, in more general terms, the kinetic energy of a freely spinning body or cluster of bodies? How does the time rate of change of kinetic energy relate to the applied external moment? We begin by defining kinetic energy.

The kinetic energy of the particle with mass m,, translating with the velocity vf relative to the arbitrary reference frame R, is defined by

(6.60)

It is a scalar. Summing over the і particles of a body B, not necessarily rigid, establishes the kinetic energy of body В wrt reference frame R :

і і

This formulation is not very useful because it requires knowledge of every parti­cle’s velocity. By introducing the c. m. В of the body, we can derive a much more practical relationship.

Theorem: With the c. m. В of a rigid body В known, the kinetic energy TBR

of body В wrt to reference frame R can be calculated from its rotational and translational parts:

tbr _ і – BRjB, br і і я,-,/?,,/?

1 =2Ш 1 Вш +2W V Bv В (O. OZ)

The rotational kinetic energy is a quadratic form of the angular velocity u>BR of the body В wrt the reference frame R and the MOI tensor IB of body B, referred to its c. m. B. The translational kinetic energy is patterned after Eq. (6.61), using the scalar product of the linear velocity of the c. m. multiplied by the total mass mB of the body. Employing the c. m. of a body in calculating the kinetic energy is just a convenience yielding the most compact formula. Any other body point could be used. An additional term makes the adjustment and leads to the same numeri­cal result (see Problem 6.11). Because the numerical value is independent of the reference point, the nomenclature TBR refers only to the body and reference frames.

Proof: We start by expanding Eq. (6.61) and using the definition of the linear

velocity vf = DRsiR, with point R an element of frame R:

YlmiVfvR = Y^miDRSiRDRsiR

І І

Now we introduce the displacement vector triangle siR — siB + sBR with В the c. m. of В:

2 TBR = J2mi(DRSiB + DRsBR)(DRsiB + DRsBR)

Because В is the c. m., the second and the third terms vanish. Why is this so? First, m, is constant, thus ]T, mjDRsiB = DR(miSiB). Second, summation and differentiation may be exchanged; therefore, DR(miSiB) = DR(^imiSiB) but 52; m;*iB = 0 is a null vector, and the rotational derivative of a null vector is zero. The last term, with the definition of the linear velocity = DRsBR, provides the

last term of Eq. (6.62). The first term needs some massaging to complete the proof. If В is rigid, DBSiB = 0, and

Y, miDRsiBDRsiB = ^т{0в$ІВ+ШЧТв){0В8ів + ftBRsiB)

І І

= 7>,nM»anB*sa,

І

After some manipulations and with the definition of the MOI tensor Eq. (6.1), we produce

uBR = G?*lW*

Moving the factor 2 to the right side confirms the first term of Eq. (6.62) and completes the proof.

For a cluster of rigid bodies Bk, k = 1, 2, 3,…, we can superimpose the indi­vidual contributions of Eq. (6.62) and obtain the total rotational and translational kinetic energies

The proof follows from the additive properties of kinetic energy.

Example 6.13 Flywheel Car

Problem. A car with mass mBt stops to recharge its flywheel (mass mBl and MOI Ig22) to the maximum permissible angular velocity шВгК. If there were no losses, what would be the maximum speed the car could achieve?

Solution. Initially, all energy is stored in the flywheel. To reach maximum velocity, the rotational energy must be fully converted into translational energy. From Eq. (6.63)

imB’ +mB2)vRvRBx=G:B2RlBBluB2R

Let us introduce a coordinate system associated with reference frame R and the following components:

ЩЙ = [У 0 0], = 10 0 r], and [lBl]R = [diag(/i,/2,/3)]

After substitution we obtain the maximum speed of the car:

V tnB’ + гпВг

A fast spinning, large wheel in a light car will provide maximum speed.

Applying a torque to a body increases its rotational kinetic energy. The energy theorem describes the phenomena.

Theorem: The time rate of change of rotational kinetic energy of a rigid body

В wrt inertial frame I equals the scalar product of the body’s angular velocity шш and the applied moment mB referred to the c. m.

d TBI

—— = шВІтв (6.64)

d t

To maximize the increase of kinetic energy, the external moment must be applied parallel to the angular velocity. Interestingly enough, the increase does not depend on the MOI of the body, but the current angular velocity.

Proof: Let us assume that point В is fixed in the inertial frame I so that we can concentrate on the rotational kinetic energy. From Eq. (6.62)

2 TBI = шшІввшш

Take the time derivative of the scalar TBI, which is equivalent to the rotational derivative wrt any frame, and specifically the body frame. Then apply the chain rule

2^£- = 2 DBTBI = DboobiIhbojbi + wBlDB(lB<jjBI)

Recognize that the first term on the right equals the second term because 1) the term is a scalar and 2) the body В is rigid, which enables us to move /f (symmetric tensor) under the rotational derivative

DBo, BIlBBooB’ = ojBrIBBDBojBI = uBlDB(lBcoBI)

Thus, introducing the angular momentum fif — ІвшВ! we get

— = QB, DB (івШш) = G>BlDBlBJ (6.65)

dr

To replace the angular momentum term by the extemal moment, we substitute Euler’s equations, transformed to the body frame DBlBB + ГlB, lBJ = mB. Because the cross product with the same vectors vanishes, the proof is completed:

—— = шв,(тв — ГlBIlBB) = QB, mB QED

An important question in gyrodynamics is the conditions for which the kinetic energy remains constant. Besides two trivial cases (mB = 0 and шВІ = 0), the kinetic energy does not change if the external moment is applied normal to the spin axis. The energy theorem is useful for the study of gyroscopic responses and leads to one of the integrals of motions.