Our heavyweight helicopter equal in the world does not have
In Rostov started production of the most load-lifting rotary-wing car The Russian holding «Helicopt[...]
Normal Shock Relations
The shock may be described as a compression front, in a supersonic flow field, across which the flow properties jump. The thickness of the shock is comparable to the mean free path of the gas molecules in the flow field. When the shock is normal to the flow direction it is called normal shock, and when it is inclined at an angle to the flow it is termed oblique shock. For a perfect gas, it is known that all the flow property ratios across a normal shock are unique functions of specific heats ratio, Y, and the upstream Mach number, M1.
Considering the normal shock shown in Figure 2.29, the following normal shock relations, assuming the flow to be one-dimensional, can be obtained:
|
m2 = 2 + <y — 1)M2 2 2yMf — (у — 1) |
(2.95) |
|
P2 = 1 + 2y, (m2 1) P1 Y + 1 V |
(2.96) |
|
Normal shock |
|
Mi |
M2 |
|
Pi |
P2 |
|
Ti |
T2 |
|
Pi |
P2 |
|
Figure 2.29 Flow through a normal shock. |
 |
 |
 |
|
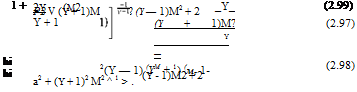In Equation (2.98), h1 and h2 are the static enthalpies upstream and downstream of the shock, respectively. The stagnation pressure ratio across a normal shock, in terms of the upstream Mach number is:
 |
 |
The change in entropy across the normal shock is given by:
