Precession and Nutation Modes

Euler’s law governs the dynamics of rotating bodies. In general, its differential equations are of sixth order, with three angular rates and three attitude angles as state variables. For bodies with constant spin rate, we are only interested in the rates and attitudes normal to the spin axis. They are governed by four first- order differential equations. If linearized by small perturbations, their characteristic equation has two conjugate complex pairs of roots, giving rise to two dynamic modes called precession and nutation.

6.4.1.1 Precession. Precession is the response of a gyroscope to a persis­tent external moment. Euler’s law reveals the nature of that response and enables us to derive a relationship between precession rate and external moment.

Consider a gyro В with angular momentum and subjected to the external moment mB. Euler’s law, Eq. (6.37), states that D1^1 = mB, i. e., the change of angular momentum is in the direction of the applied moment. Expressed in inertial coordinates and dropping the sub – and superscripts,

Integrated,

We evaluate the integral by dividing it into time increments At during which the moment can be considered constant:

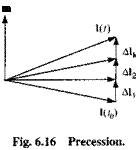
[lit)]1 = Vito)]’ + ^[mk]‘ At

With fmic]1 At = [Д/fc]7 the last term becomes

[lit)]1 = Vito)]1 +

к

Figure 6.16 shows the integration process. The incremental angular momentum [AIk]1 is collinear with the instantaneous moment [mkY. Overall, the angular momentum vector [lit)}1 lines up with the moment vector. For a fast gyro for which the spin axis, the angular velocity vector, and the angular momentum vector
are close together, one can verbalize that the body axis tries to align itself with the moment vector.

This motion is called precession. It is the slower one of the dynamic modes of a gyro and poorly understood. You probably have been at a science museum where you could not resist taking a seat on a turntable and grabbing a spinning flywheel by its handles. As you try to bank the flywheel, your seat starts to rotate on the turntable. You get off and explain to your son that this demonstrates the weird behavior of a gyroscope. It would be better to tell him that you experienced a precession in response to the torque you applied to the flywheel and encourage him to ask his physics teacher to fill in the details.

To get a quantitative relationship between moment and precession rate, we go back to Eq. (6.37) and introduce the precession frame P. This frame stays with the precessing angular momentum vector. Shifting the rotational derivative to P produces

DplBJ + np, lBJ = mB

If the magnitude of is constant and because the vector lBB1 remains fixed in P, the rotational time derivative vanishes. The equation of the precession rate ГlPI is therefore

SlPIlBJ = mB (6.57)

This vector product establishes the right-handed rule of precession.

With Eq. (6.57) you can tell your son in advance how to apply the moment in order for the turntable to turn to the left. Turning to the left means the precession vector points up; and if the flywheel’s angular velocity vector points right, the cross product tells you to generate a forward-pointing moment vector. Grab the wheel, push the right handle down and the left one up. You will be become an instant hero.

6.4.1.2 Nutation. Nutation is the response of a gyro to an impulse. Consider the free gyro in Fig. 6.17. We subject the gyro for a short time Дt to the moment mB = 2Sab/ and observe its reaction. According to Euler’s law [Eq. (6.56)], the change of angular momentum as a result of the impulsive moment is

[Al]1 = [Щ)]1 – [l(t0)Y = [mB]! At

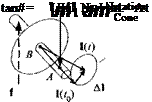During At, the angular momentum vector jumps from [/(fo)]7 to [1(f)]1. The body axis, held back by the body’s inertia, is still in its original position and starts to respond by revolving around the new location of the angular momentum, tracing out the half cone angle в:

The greater the impulse and the smaller the initial angular momentum are, the greater this nutation cone becomes. Initially, the body axis yields in the direction of / but returns to its original position through the nutation cycle. On the average the body axis evades the impulsive force perpendicularly. For many successive impulses a fast gyro with small nutational motions appears to move normal to the applied force. In the limit precession can be thought of as a sequence of infinitesimally small nutations caused by a sequence of impulses.

Let us play with the top, whose dynamic Eq. (6.47) we derived earlier. It is spinning on the ground about the vertical. We shake it out of its complacency by imparting an impulsive moment with our whip. The top starts to wobble, but refuses to fall down. The higher its spin rate (angular momentum) the smaller the nutation angle and the greater its resistance to our onslaught. We witness the inherent stability of spinning objects to perturbations. Several technical applications make use of this feature. I already introduced the dual-spin spacecraft in Example 6.11, and in Chapter 10 I will derive the equations of motion for spinning missiles and Magnus rotors.