Translational helicopter flight
It is assumed that the effect of the actuator disc used to approximate the rotor is to add incremental velocities vy and z^, vertically and horizontally respectively, at the disc. It is further assumed, in accordance with the simple axial momentum theory of Section 9.1, that in the slipstream well behind the disc these incremental velocities increase to 2vy and 2respectively. The resultant speed through the disc is denoted by U and the resultant speed in the fully developed slipstream by U. Then, by considering vertical momentum:
|
W = pAU(2uv) = 2 pAUvy |
(9.52) |
|
Also, from the vector addition of velocities: |
|
|
U2 — {V + Vh)2 + (z’v)2 |
(9.53) |
|
where V is the speed of horizontal flight. By consideration of horizontal momentum |
|
|
^pV2ACD = 2pAUvh |
(9.54) |
|
where Co is the drag coefficient of the fuselage, etc., based on the rotor area A. Power input = rate of increase of KE, i. e. |
|
|
P=X-pAU{U2-V2) |
(9.55) |
|
and from vector addition of velocities: |
|
|
U2 = {V + 2uh)1 + {2uy)2 |
(9.56) |
|
The most useful solution of the five equations Eqn (9.52) to Eqn (9.56) inclusive is obtained by eliminating U, Vh and zv |
|
|
W Vy~ 2pAU |
(9.52a) |
|
pV2ACo Co y2 h 2 pAU 4U |
(9.54a) |
Then, from Eqn (9.53):
U2 = Vі + 2Vvh + vl + v2 Substituting for vy and z^, and multiplying by U2 gives
Introducing the effective disc loading, /<je, from Eqn (9.48) leads to
(9.57)
a quartic equation for U in terms of given quantities. Since, from Eqn (9.56),
![]() ■ 4Vi>h + 4i>l + 4i>l
■ 4Vi>h + 4i>l + 4i>l
Then
|
4С°У’+-6<*и Uyip0J |
![]()
P=X-pAU{U-V2) = X-pAU[4Vvb+4vl
which, with the value of U calculated from Eqn (9.57) and the given quantities, may be used to calculate the power required.
Example 9.6 A helicopter weighs 24 000 N and has a single rotor of 15 m diameter. Using momentum theory, estimate the power required for level flight at a speed of 15ms-1 at sea level. The drag coefficient, based on the rotor area, is 0.006.
A =t(15)2 = 176.7m2 4
, W 24000 ,
/de =~r = —r= ,36Nm
Aa 176.7 x 1
Idc 136 2
= о—- = 55-6 m s
2po 2 x 1.226
With the above values, and with V = 15ms_1, Eqn (9.57) is
![]() t/4 – 225U2 – l – U(0.006)(3375) = (55.6)2 +
t/4 – 225U2 – l – U(0.006)(3375) = (55.6)2 +
2 16
l. e.
U4 – 225U2- 10.1256/ = 3091
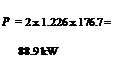 |
|
This quartic equation in U may be solved by any of the standard methods (e. g. Newton – Raphson), the solution being U = 15.45ms-1 to four significant figures. Then
This is the power required if the rotor behaves as an ideal actuator disc. A practical rotor would require considerably more power than this.











