Two Approaches

Just as Newton’s second law describes the translational degrees of freedom of a flight vehicle so does Euler’s law govern the attitude degrees of freedom. Its origin is attributed to Euler and is considered either a consequence of Newton’s law (Goldstein) or a fundamentally new principle of dynamics (Truesdell).

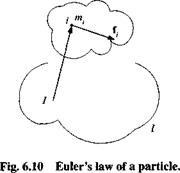
6.3.1.1 Euler’s Law according to Truesdell. Truesdell,1 having conducted a thorough historical research, concluded that Euler’s law in its embryonic form is based on a publication by Jakob Bernoulli (1686), predating the Newtonian laws by one year. Euler polished Bernoulli’s ideas and formulated the angular momentum law as an independent principle of mechanics in 1744. In its elementary form we state it first for a particle (refer to Fig. 6.10).

The inertial time rate of change of angular momentum about a point is equal to and in the direction of the impressed moment about the same point. Consider a particle m,-, displaced from the reference point I by s,-/ and moving with the linear velocity v wrt the inertial frame I. Its angular momentum is Vu — niiSuV-, and the impressed moment relative to point I is т. ц = S,■//,-, where /; is the force acting on the particle.

Euler’s law for such a particle states that the time rate of change wrt the inertial frame I of the angular momentum lj equals the external moment mu:

D’llj = mu (6.32)

and expanded

(6.33)

On each side of the equation is a vector product of the displacement vector s u with either the linear velocity vf (related to the displacement vector by v = D/s,/) or the force /,.

We introduced a new vector, the moment Шц acting on particle і wrt a point 1. It should not be confused with the scalar m;, the mass of particle і. Now let us turn to the other interpretation.