Aerodynamic cross coupling

Just as for aircraft, it is difficult to model the aerodynamic forces of missiles in a form that can be analyzed and eval­uated quantitatively. Because the functional form is not known, the aerodynamic functions are expanded in a Taylor series in terms of the state variables relative to a reference flight. To capture the rolling and other cross-coupling effects, we have to include at least second-order derivatives.

Let us go back to Sec. 7.3.1 to sort out the existence of the derivatives. The tetragonal symmetry of our missile implies that certain derivatives are vanishing. The expansion of the aerodynamic force and moment perturbations Y, Z, L, M, N is carried out up to second order. Those that survive the symmetry test are listed in Table 7.3. The derivatives in the x direction are disregarded because we maintain the Mach-number dependency in tabular form.

The second column of Table 7.3 displays all of the familiar linear derivatives, whereas the remaining columns show the second-order derivatives. Notice that all of the second-order derivatives of the yaw and pitch channels are dependent either on roll rate p or roll control deflection Sp. The rolling moment itself is a function of incidence angles (represented by v and w), yaw, pitch rate (r, q) coupling, and the effects of yaw, pitch control (Sr, Sq).

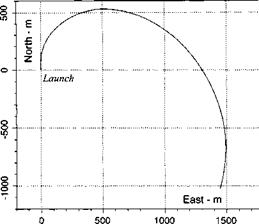
As a practical example, consider an air-to-air missile, executing a lateral ma­neuver toward an intercept (see Fig. 7.4). To generate the lateral acceleration, the airframe develops v or, equivalently, sideslip angle. Although the missile does not roll to execute the maneuver, the roll channel will be excited by the aerodynamic coupling, assuming the vertical channel is also active. There will be vertical chan­nel transients because w or, equivalently, angle of attack is necessary to maintain altitude. Once the roll DoF is stirred, it couples back into the longitudinal and lateral channels.

In the example all of the first – and second-order derivatives play a part, with the control effectiveness derivatives excited by the control fin deflections. It is easy to

cogitate about these yaw/pitch/roll cross-coupling effect, but the difficult part is to flesh out the skeleton of Table 7.3 with numerical values. Particularly challenging are wind-tunnel tests that measure unsteady derivatives associated with the body rates p, q,r and the incidence rates ii, w.

For our limited discussion we focus on the important Lwv derivative that causes roll torques in the presence of angle of attack and sideslip angle. Once the roll rate is stirred, we investigate the inertial coupling into the yaw channel in the presence of pitch rate.

To test the coupling effects, I use the CADAC SRAAM6 simulation, a generic air-to-air missile. I keep its rather complex aerodynamic model and the propulsion subroutine, but bypass the guidance and control loops completely. Fortunately, the missile airframe is aerodynamically stable—though somewhat oscillatory—thus enabling open-loop computer runs.