Aerodynamic expansions

The aerodynamic force is chosen as axial, side, and normal components in agreement with standard wind-tunnel con­ventions and the appropriate sign changes. There is no sign change in the moments. To prevent confusion with the normal force, the yawing moment is labeled LN.

efa)T~		‘-a’		(єта)Вр		~ L ~
	=	Y		(єта)Вр	~	M
>/«)?		-N		(єта)1Р		LN L J

As practiced before, we expand the aerodynamic perturbations into Taylor series. From Fig. 7.1 we determine the linear derivatives for planar vehicles as

9A ЭА dA 9A 9A 9A

A — —и H——————— w H——- <7 H—— и H—— w H—— de

du dw dq du dw dSe

dY dY dY dY dY dY

Y = —— v + — p + — r 4—— v ——da ———– dr

dv dp dr di) dda ddr

Ar dN dN dN dN dN dN

N =——- и H—- w H—— о H—– й H—– w H—– de

du dw dq du dw dde

dL dL dL dL dL dL

L = —v ——— p 4— r + —v H——- da ——– dr

dv dp dr di) dda ddr

dM dM dM dM dM dM

du dw dq4 du dw dde

Based on experimental evidence, the underlined terms are neglected, and the as­sumption is made that the acceleration terms, underlined twice, can be absorbed in the corresponding damping derivatives.

Wind-tunnel test data are usually presented as functions of Mach number M, angle of attack a, and sideslip angle /3, rather than the velocity components к, v, w. As before, we can expand the derivatives in terms of a and /3 and then replace a — w / Vr and ft = vjVr in order to reintroduce the state variables w and v (with small-angle assumption and Vr the reference speed).

Replacing the и dependence by the Mach number is more complicated and takes a few steps. Let us start with the definition of the nondimensional axial derivative

A = pV2SCA

The partial derivative relative to и has two terms, evaluated at reference conditions

dV	1 i2 эслэм
= PrVrSC A — r ou	r 2 dM ou r

The first partial dV/du = 1 because V and и are changing by the same amount (small-angle assumption) and similarly dM/du = dV/{adи) = I /a (a is sonic speed). Therefore, with the dynamic pressure designated qr

suitable to receive experimental data

^ = (prVrSCA, + – Cam ju + -——Ca^w + qrSCASeSe V &r / V r

N — { pTVTSCNr H—– С^м Jm + ^—-C^w + qrSC^Se8e

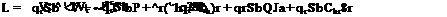
ar / Vr

w c n. 4rSc qrSc

Рг*г$сСтг – j – Сцім 1U CmaW

a, / Vr

H—2у (^ra« + qrScCm/je8e

+ qrSbC„Sa8a + qrSbC„Sr8r

All derivatives were nondimensionalized with the help of the reference area S, the chord c, and span b for longitudinal and lateral derivatives, respectively. The subscript r indicates the variables associated with the reference trajectory. They are in general a function of time. As an exception, however, the subscript r in the derivatives C/r and C„r refers to the perturbed yaw rate of the vehicle.

The coefficients of the reference trajectory CAr, C’Nr, and Cmr show up in the longitudinal aerodynamics of A, A, and M in conjunction with the forward velocity perturbation u. They are known functions of time. The terms in which they occur account for the fact that the dynamic pressure is increased (to the first order) by prVru, as we conclude from the following:

<Vr + uf * + 2Vru) = ^ + prVru

For steady reference flight the reference pitching moment Cmr is zero. However, for our pull-up and pushdown maneuvers, a reference pitching moment exists, and therefore the Cmr term should be included in the equations.

Herewith, we completed the modeling of the aerodynamics for the unsteady per­turbation equations. During the derivation, I made quite a few simplifying short­cuts. Only linear terms describe the model, and even some of these derivatives were assumed negligible based on some rather sketchy test results. Furthermore, the bending of the lifting surfaces, which could be quite substantial during high load factors, was not discussed, but could have been included in the derivatives Cjv„, Ст„, and C/,,. Yet we did accomplish our objective, i. e., to derive the un­steady perturbation equations in state-variable form for the vertical pull-up and push-down maneuvers for aircraft or cruise missiles. What remains is the summary of the results.

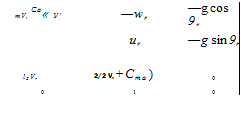
State equations of vertical maneuvers.

The perturbation equa­tions of unsteady vertical maneuvers can finally be written in the desired matrix form by combining Eqs. (7.75) with (7.77) and (7.76) with (7.78). The six differ­ential equations are augmented by the integrals ф, в, and ф of the angular rates p, q, and r. As we inspect the nine differential equations, we discover that they can be decoupled into two sets of longitudinal and lateral equations. The longitudinal state vector is composed of u, w,q, and в, and the lateral state vector consists of the remaining v, р, г,ф, and ф variables.

with /[j = (/ц/33 – ф/Ізз, /33 = (hil33 – In)/hi – Now we have five linear differential equations in the lateral velocity component v, the roll and yaw rates p and r, and the derivative roll and yaw angles ф — p, ф = r. Notice how the reference pitch rate qr multiplied by a rather complicated ratio of the MOI components affects the rolling and yawing equations. Furthermore, the aileron and rudder controls couple into the yawing and rolling equations.

The matrix of Eq. (7.80) has the undesirable characteristic that its determinant is singular. You can verify that fact by multiplying the last two columns by g sin 9r and g cos 9r, respectively, and subtracting column 5 from column 4. The last column of the determinant is zero. A rank deficient matrix like this will cause you problems when you calculate its eigenvalues or try to control all of the state variables.

Fortunately, we can avoid that hazard by replacing the roll and yaw angles with the horizontal perturbation roll angle a. I will show you how to proceed. Because the angular perturbations are small angles, we can write them as an angular vector with the components ф, 9, and ф in the reference body coordinates. Transforming this angular vector into inertial coordinates (local level coordinates), using Eq. (7.74), we obtain the horizontal component a:

1 b Ф I	= [f]Brl	Ф 9	=	cos 9r 0 sin 9,- 0 1 0		Ф 9
r		Ф		—sin 9r 0 cos 9r		f

ф cos вг + ф sin 9r = 9

—ф sin 9r + ф cos 9r

After taking the time derivative

a = ф cos 9r + ф sin 9r = p cos 9r + r sin 9r

we replace the last two rows in Eq. (7.80), delete the last column, and replace the first element in the fourth column by g. The nonsingular lateral equations are now

qrS mVr	wr	—ur	g
qrSb vr b	qrSb2 p 21’nVrh	~ 1 QrSb2 f1 г’ qr + +cb>	0
qrSb s~< Тъ~^Ггп$	(/ll — /2)+^ 1 qrSb2 Ф <1г+2фУ’П<’	2/’3Vr ^»r ^ ‘-‘"pS	0
0	COS er	sin er	0

Equations (7.79) and (7.81) are the preferred set of perturbation equations for vertical maneuvers, although we have to come to grips with the horizontal roll angle a.

The lateral and longitudinal equations are formulated in body-fixed coordinates. Their state vectors are the linear and angular velocity components parallel to the perturbed body axes. This form is most convenient for feedback control analysis because the state vector components and their time derivatives can be directly measured by onboard sensors. Note, however, that the state vector represents the perturbations from the reference trajectory. Therefore, only for the lateral equations can the state vector be measured directly. The measurements of the longitudinal variables contain both the reference and perturbation values. For flight-test data matching the reference values must be subtracted from the measurements to obtain the longitudinal perturbations.

Equations (7.79-7.81) can also serve as perturbation equations of steady flight. All you have to do is set qr = 0. Moreover, if the reference flight is horizontal, wr = 0, sin 0, = 0, cos 0r = 1, the equations are particularly simple. Finally, I hope that the derivation of the equations of motions for aircraft and cruise missiles during pull-up or push-down maneuvers gives you a good perception of the modeling of flight vehicle perturbations.