Derivative maps

As you build your aerodynamic model, you have to apply the vanishing-derivative rules numerous times. Just for the linear deriva­tives it would be 72 times. To save you time, I supply maps that let you determine the existence of derivatives by inspection of their grid pattern. They apply for up to third-order derivatives for aircraft and up to second-order derivatives for missiles.

Figure 7.1 graphically patterns Eq. (7.51) and the associated Rule 1 for planar vehicle derivatives up to third order. In the following discussion, however, rather than referring to the vanishing derivatives, I will emphasize those that survive the sifting process.

Depending on the force components і, the order of the derivative, and the even or odd integer of the third superscript, the existence of the derivative is indicated by two symbols—cruciform or box—in the top table of Fig. 7.1. For instance, for the first-order derivative Xu the table assigns a cruciform symbol to the force compo­nent X. To determine existence, refer to the single row array. Because Xu is asso­ciated with a cruciform symbol, it exists. However, Xv, having a box symbol in the array, vanishes because it does not show the required cruciform symbol of the table. Moving into the next column of the table, the first order derivative Lgp must have a box symbol. The single array confirms its existence. You can use this array to deter­mine quickly, which derivatives you must include in you linear aerodynamic model.

For second-order derivatives D’n the symbols are reversed in the table of Fig. 7.1, and the 12 x 12 array is used to determine their existence. The array is symmetric because the order of taking partial derivatives is irrelevant (assum­ing continuous functions). Therefore, you can start with either rows or columns. For example, Zwsq, requiring the box symbol, exists according to the array, but Ywgq, associated with the cruciform pattern, vanishes. About 198 second-order derivatives exist. It is up to the aerodynamicist to determine their significance and magnitude. Hopefully, if called to model nonlinear effects, you can neglect most of them, but only after you have reasoned through all exclusions.

Third-order derivatives must be separated into two groups, depending on an even or odd third-order superscript (even or odd refers to the position number of the variable in the state vector). If the last superscript is even, e. g., v, the cruciform

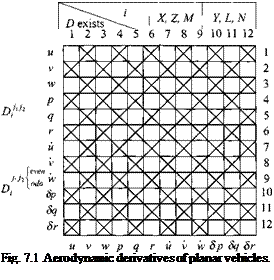symbol is associated with a derivative such as Zwrv. Entering the square array with w and r indicates existence of that derivative. Let us check out our first example LUqSq — D511 of Eq. (7.47) for planar vehicles. Its third superscript is odd, and because L is in the second column, the cruciform symbol applies. The square array entry with и and q requires the box symbol; therefore, the derivative vanishes.

For vehicles with tetragonal symmetry, a compact graphic display is possible only for first – and second-order derivatives. Figure 7.2 summarizes both Eqs. (7.51) and (7.52) or Rules 1 and 2. The table in Fig. 7.2 assigns different symbols for the existence of four groups of derivatives. For instance, Xu exists, and Xv vanishes; Zuw survives, but Zusp does not. I am sure by now you have caught on to my scheme.

The graphical aids of both figures can be used to determine uniquely the existence or nonexistence of aerodynamic derivatives. A significant number of derivatives can be eliminated by symmetry alone. Reflectional symmetry eliminates about half of the linear candidates, and because the square array is symmetrical, only approximately a quarter of the second – and third-order derivatives need be consid­ered. For vehicles with tetragonal symmetry, these numbers are further reduced by a factor of one-half.

I already mentioned earlier that some of the state variables could also be replaced by other relevant quantities. Particularly, the substitutions of a for w and ft for v are

quite common. Also и is often replaced by the Mach-number dependence. Similar alternatives are used for w —> a and v —> $. The controls Sp. Sq, Sr refer either to the missile’s roll, pitch, and yaw or the aircraft’s aileron, elevator, and rudder.

The coordinate system of the expansion variables is the dynamic system. In most cases the body coordinates serve as the dynamic system. For an aircraft in steady flight, the reference body axes are the inertial axes, and during its perturbed flight the body axes become the coordinate system for the aerodynamic expansion. Fre­quently, the stability axes (special body axes) are used. However, other possibilities must also be considered. For a spinning missile the dynamic coordinates are as­sociated with the nonspinning body frame. Because this glove-like frame also has rotational symmetry, the derivatives are expressed in these coordinates, and Rule 2 applies. A similar situation exists for Magnus rotors (see Sec. 10.1.1.4) or spinning golf balls. Their spin axes, however, are essentially normal to the velocity vector. Thus the nonspinning frame exhibits planar symmetry, and Rule 1 should be used.

The modeling of the aerodynamics for computer simulations frequently includes tabular look-up for variables with large variations, and the Taylor expansion is only carried out for those variables that remain small. So far, we have dealt with complete expansions of all 12 components of the state vector. With minor modifications the results are applicable also to these incomplete expansions.

For instance, if the aerodynamics is expressed as tabular functions of the ve­locity component u, the Taylor series is carried out in terms of the state variable components 2 through 12 only. All derivatives remain implicit functions of u, and
the order of the derivatives is reduced by one. For example, an aircraft’s Xwsq(u) derivative is modeled by a one-dimensional table. Instead of a table, it also could be completely expanded in powers of u, provided the polynomial fits the data:

Xwbq^M) — Xuw$qU -|- Xu2wfiqU -|- Xulw$qU -|-

Please confirm the existence of the derivatives on the left – and the right-hand sides.

This procedure applies to any derivative and any state variable component. Also more than one variable can be replaced by implicit functions. We will use this approach in several instances. In Sec. 10.2.1 you will see it applied to aircraft and missile six-DoF models. For the CADAC FALCON6 simulation I will introduce reduced derivatives that are implicit functions of Mach, angle of attack, and, in some cases, also of sideslip angle. The CADAC SRAAM6 air-to-air missile model, using aeroballistic instead of body axes, can also be pressed into this scheme, and you will see that most derivatives are implicit functions of Mach and total angle of attack. Finally, the CADAC GHAME6 hypersonic vehicle is a straight expansion of derivatives with Mach and angle of attack as implicit variables.

The most frequently encountered task, however, is the linear expansion of the aerodynamic derivatives. I will demonstrate the procedure for the linear perturba­tion equations of steady flight and specifically derive some simple state equations that are needed for our autopilot designs in Sec. 10.2.2. A further sophistication is the extension to unsteady flight like missiles in pushover and terminal dive or in lateral turns.