Flight-Path-Angle State Equations

For the design of a flight-path-angle tracker, we need the pitch dynamics ex­pressed in flight path angle у, pitch rate q, and its integral, pitch angle 9. Because this autopilot function is primarily for an aircraft, we take a slightly different ap­proach than in the preceding section. The lift force replaces the normal force. Therefore, the left-hand side of the third component of Eq. (7.55) mw is replaced by mVy, using the relationship [Eq. (7.62)]

mw — — та — —mV у

and the right-hand aerodynamics is formulated in terms of the lift force L. The symmetry conditions of the expansion Rule 1 apply as well for the lift as the normal force, but, alas, we have to put up with confusing notation. Aircraft aerodynamicists prefer lift to normal force and use L instead of Z or —A. They designate the rolling moment as LL, the convention we used earlier. From Fig. 7.1 we derive the linear derivatives and neglect the coupling and gravitational terms

mVу — Luu + Laot + Lqq + Ьйй + L^a + L$e8e (7.72)

Comparison with Eq. (7.59) shows that a tetragonal missile lacks the и derivatives. We neglect these m-dependent derivatives for the aircraft, and the damping effects La and L„ as well. By replacing a with a — 9-у, we succeed in deriving one of the state equations, after having absorbed m in the denominator of the derivatives:

La, L&e

— у Л—— oe

V У V

The other state equations follow directly form Eq. (7.58):

q — Mqq + Ma9 — May + M$e 8e

Both equations combined yield the desired flight-path-angle formulation

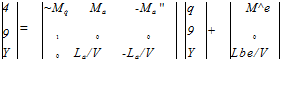
(7.73)

where the dimensional derivatives are calculated from the nondimensional deriva­tives according to

These equations, in state variable format, are used in Sec. 10.2.2.6 to develop a self-adaptive flight-path-angle tracker. I am always amazed how plant equations, as simple as Eq. (7.73), produce useful models for autopilot designs, which can be implemented in six-DoF simulations.

These examples should be enough to help you develop other linear models for aerospace vehicles. We covered the roll transfer function, pitch dynamics expressed in normal acceleration, and flight-path-angle dynamics. You should be able to derive the yawing equations, the roll/yaw coupled dynamics, and the full linear stability equations of steady flight. We turn now to applications of unsteady flight.