Our heavyweight helicopter equal in the world does not have
In Rostov started production of the most load-lifting rotary-wing car The Russian holding «Helicopt[...]
Flow with Friction
In the Section 2.13.4, on flow with area change, it was assumed that the changes in flow properties, for compressible flow of gases in ducts, were brought about solely by area change. That is, the effects of viscosity and heat transfer have been neglected. But, in practical flow situations like, stationary power plants, aircraft engines, high vacuum technology, transport of natural gas in long pipe lines, transport of fluids in chemical process plants, and various types of flow systems, the high-speed flow travels through passages of considerable length and hence the effects of viscosity (friction) cannot be neglected for such flows. In many practical flow situations, friction can even have a decisive effect on the resultant flow characteristics.
Consider one-dimensional steady flow of a perfect gas with constant specific heats through a constant area duct. Assume that there is neither external heat exchange nor external shaft work and the difference in elevation produces negligible changes in flow properties compared to frictional effects. The flow with the above said conditions, namely adiabatic flow with no external work, is called Fanno line Bow. For Fanno line flow, the wall friction (due to viscosity) is the chief factor bringing about changes in flow properties.
Working Formulae for Fanno Type Flow
Consider the flow of a perfect gas through a constant area duct shown in Figure 2.31. Choosing an infinitesimal control volume as shown in the figure, the relation between Mach number M and friction
 |
 |
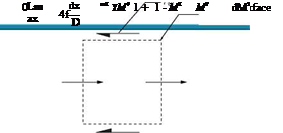factor f can be written as:
In this relation, the integration limits are taken as (1) the section where the Mach number is M, and the length x is arbitrarily set equal to zero, and (2) the section where Mach number is unity and x is the maximum possible length of duct, Lmax and D is the hydraulic diameter, defined as:
4 (cross-sectional area)
wetted perimeter
 |
 |
 |
 |
On integration, Equation (2.108) yields:
where f is the mean friction coefficient with respect to duct length, defined by:
L max
fdx.
 |
 |
 |
 |
 |
|||
Likewise, the local flow properties can be found in terms of local Mach number. Indicating the properties at M = 1 with superscripted with “asterisk,” and integrating between the duct sections with M = M and M = 1, the following relations can be obtained [2]:
