Introduction to helicopter. dynamics

The basic principle of wings, rotors and airscrews is that they accelerate a mass of air and that the resultant lift or thrust is the Newtonian reaction to that acceleration. Producing sufficient lift to permit a helicopter to fly is only a matter of having enough power to accelerate the air mass without excessive weight. A practical helicopter must, however, be able to control that lift precisely or it would be dangerous.

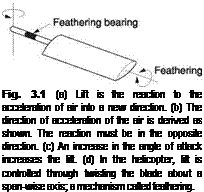
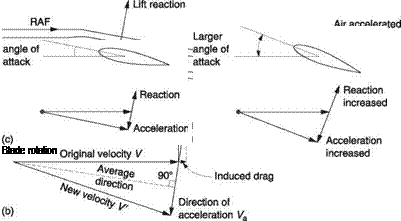
Any structure placed in a flow of air for the purpose of generating lift is called an aerofoil or airfoil. Aeroplanes and helicopters can fly when there is a wind blowing and can climb or lose height in the process. In helicopters the rotor blades have airspeed due to their rotation. Thus there can be situations where the airfoil moves through the air, or where the air moves past the airfoil. All that matters from the point of view of generating lift is the relative velocity and the direction from which it appears to be approaching the airfoil. Figure 3.1(a) shows that this is known as a relative airflow (RAF). RAF is a vector quantity as it has speed and direction. Figure 3.1 further shows that a flat plate will produce lift if it is slightly inclined to the RAF at an angle of attack. When the airfoil changes the direction of air flowing by, this represents a change of velocity and so is classed as acceleration. The reaction to that acceleration will point in the opposite direction.

Figure 3.1(b) shows how the direction of the reaction is found. For the time being, the air is assumed to be inviscid (having no viscosity). The relative airspeed does not change, only the direction, so the velocity vector V is changed to V’. The acceleration to change V to V’ must have been in the direction of the vector Va so the reaction must be in the opposite direction. It can be seen that this is at right angles to the average airflow direction. The blade reaction is the only actual force present. In fixed-wing aircraft studies, the reaction is traditionally resolved into two components: that which is measured at right angles to the RAF and called the lift, and that which is measured along the direction of the RAF and called the induced drag. In cruise lift will be vertical and drag will be horizontal.

Figure 3.1(c) shows that the lift can be increased by increasing the angle of attack since this has the effect of increasing the change of velocity. In the aeroplane, the angle of attack is controlled by alteration of the attitude of the entire machine with the elevators. In a helicopter the blades are mounted on bearings in the rotor head that

(d)

allows them to turn about a radial axis as can be seen in Figure 3.1(d). This mechanism is known as feathering.

When the relative velocity alone is doubled with respect to the case in (b), the vector Va representing the change of velocity is doubled. As the air is moving twice as fast, the wing accelerates the air in half the previous time. Achieving double the velocity in half the time means that the reaction is increased by a factor of four. In other words, the reaction is proportional to the square of the velocity. In practice four times as much lift would be quite unnecessary to balance the weight of the machine and instead, as the relative velocity doubled, the angle of attack would be reduced to about one-quarter of the previous value. This is the mechanism by which aircraft obtain the same lift over a range of airspeeds.

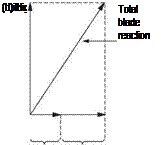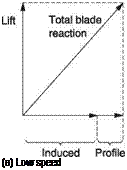
Fig. 3.2 Profile drag must be included in the behaviour of any real airfoil. The induced drag and profile drag add to tilt the total blade reaction backwards. Conditions at low airspeed are shown in (a). At a higher speed, (b), the profile drag is greater, but the induced drag is less. This is only possible because it is not really a drag.

In practice the air also has viscosity that resists movement as a function of the surface area of any body moved through it. The loss due to this effect is called profile drag. The profile drag tilts the blade reaction further to the rear as in Figure 3.2(a). There is a boundary layer between a moving object and the stationary air. At the leading edge, the speed difference across the boundary layer is maximal and the drag is greatest. Further back, the viscosity has been able to get the boundary layer moving and the drag is reduced. Thus the drag experienced by a wing or rotor blade is a function not just of the surface area but also of the chord. Very small objects possess disproportionately high profile drag, which is why the wind can blow sand but not rocks. Reynolds numbers are used to describe the relationship between dimensions and profile drag. It is important in model testing that the airspeed used is scaled correctly. Scale speed is not used. Instead the speed is chosen to produce the same Reynolds number in the model as in the full-sized device and then the drag of the model will be representative.

If an airfoil is not producing lift, the induced drag will be zero and only the profile drag will be observed. In a full-size helicopter in the hover roughly 30% of the rotor shaft power is lost to profile drag, the rest goes in accelerating the air downwards. In model helicopters and full-sized tail rotors profile power is proportionately greater as the small-chord blades operate with adverse Reynolds numbers.

Figure 3.2(b) shows the production of the same lift at a higher relative velocity. The profile drag has increased but the induced drag has reduced. This is not what one would expect from a true source of drag. The explanation is that the airfoil is an actuator or transducer, which accepts mechanical power as the product of the mechan­ical impedance and the relative velocity in order to drive the air against aerodynamic impedance. Accelerating air downwards constantly provides lift. The actuator reflects the aerodynamic impedance back as mechanical impedance. The variation in angle of attack is analogous to changing the turns ratio of a transformer or the ratio of a gear­box. Clearly if the relative velocity goes up, to keep the power the same the impedance must fall.

Once the concept of an airfoil as an actuator is understood, it is a small step to appreciate that most types of actuator are reversible. Some helicopters use an electric motor to start the engine when that motor becomes a generator. In a turbine engine, the rotating blades in the compressor are putting energy into the air, whereas the rotating
blades in the power turbine are taking energy out of the gas flow. Given this reversibility, we can immediately see how in a glider or in an autorotating helicopter the power flow through the actuator reverses. In descending through the air the wing or rotor delivers power extracted from loss of potential energy and this power is used to overcome profile drag. The glider can maintain airspeed and the helicopter can maintain rotor speed with no engine power.

The act of turning the airflow also results in rotational energy being imparted to the passing air. Conceptually, the airflow can be divided into two flows. One is the steady flow past the blade and the other is the rotational component that in the absence of the steady flow would rotate around the blade. This is known as circulation and it is proportional to the lift. In vortex theory, the circulation of an airfoil is calculated and the lift follows from that.

A further consequence of the change of direction is that the horizontal component of the relative velocity is reduced. It follows from the rearward inclination of the blade reaction that there must be a forward component of the acceleration imparted to the air. Air does not go straight down from a hovering rotor; it also revolves in the same direc­tion the rotor turns, but much more slowly: a phenomenon known as swirl. Swirl is considered in section 3.14.

It is more efficient gradually to accelerate the air down rather than have it suddenly find an inclined plate. Air passing the top edge of a flat plate cannot change direction quickly enough and the flow separates and becomes turbulent. These are the reasons for curving or cambering an airfoil. Furthermore, practical wings must contain structural members such as spars, and the thickness will be increased to accommodate them. The thickness is contained within a streamlined shape to reduce drag.

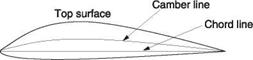
Figure 3.3(a) shows a streamlined cambered section. The mean camber line is half way between the upper and lower surfaces. The chord line joins the ends of the camber line. The angle of attack is the angle between the chord line and the relative airflow. The camber of the airfoil can be optimized for the speed range of interest. For high lift at low speeds, the camber will be heavy in order to make Va as large as possible.

Bottom surface (a) Cambered section

Camber and chord line (b) Symmetrical section Fig. 3.3 Both cambered and flat airfoils will produce lift. In practice they will be thickened to reduce separation and to allow structural components to be incorporated. Cambered airfoils work best at low speeds. In the cambered section (a) the camber line will curve away from the straight chord line. In the symmetrical section (b) the chord line and camber line coincide. A symmetrical airfoil is equally capable of producing lift upwards or downwards. With zero angle of attack there is no induced drag, only profile drag.

Clearly such a wing will be creating a lot of drag at the small angles of attack needed at high speeds. For high speed operation, the camber will need to be very small, but this kind of wing will be inefficient if used at large angles of attack at low speed, hence the use of flaps on fixed-wing aircraft. With a cambered section, air is still accelerated downwards leaving the section even when the angle of attack is zero, and so a slight negative angle of attack is necessary to obtain the zero lift condition.

Figure 3.3(b) shows a symmetrical section in which the camber line and the chord line are one and the same. A symmetrical section is a streamlined flat plate. The curvature prevents separation over the leading edge. At zero angle of attack, the airflow is also symmetrical, and no net air reaction results. There is thus no induced drag, only profile drag. If the angle of attack is made positive, air is accelerated down, and the reaction is upwards. If the angle of attack is made negative, air is accelerated up and the reaction is downwards.

The reader is cautioned against explanations of the origin of lift based on Bernouilli’s theorem. Bernouilli made it quite clear that his theorem relates to conservation of energy in flowing air such that the sum of the static and dynamic pressures remains constant. Bernouilli’s theorem only applies if no energy is put into the air. However, a wing or a rotor blade is an actuator that is exchanging energy with the air. This is clear from the presence of induced drag. When energy is put into the airflow, Bernouilli’s theorem simply doesn’t apply and the explanations based on it are flawed and should be disregarded.

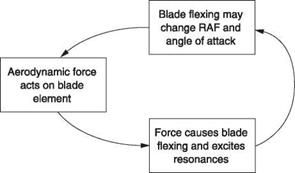
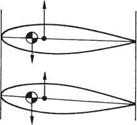
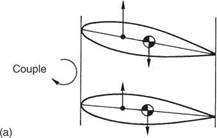
The lift developed by the blades is distributed over the chord, but not uniformly. The centre of pressure is where a single force would act producing the same effect as the distributed lift. In real airfoil sections, the centre of pressure is ahead of the mid-chord point. If the blade is made of a material with uniform density, the centre of pressure will be ahead of the centre of mass and, as Figure 3.4(a) shows, a couple results. This couple would tend to twist the blade and increase the angle of attack, making the lift greater and increasing the twist further. In extreme cases the blade will flutter; a violent condition that will usually destroy any structure suffering from it.

In aircraft, wings can usually be made rigid enough to prevent flutter, but this cannot be done with the long thin blades of the helicopter. The solution universally adopted is to construct the blade so that the mass centroid (see Chapter 2) of the blade is ahead of

Fig. 3.4 (a) If the centre of lift is ahead of the CM, lift tends to increase the angle of attack. (b) If the centre of lift is behind the CM, lift tends to reduce the angle of attack: a stable condition.

the local centre of pressure. As Figure 3.4(b) shows, this results in a stable blade, since an increase in angle of attack producing more lift tends to generate a couple reducing the angle of attack.

The airfoil section selected for a helicopter blade will be a compromise to satisfy a number of conflicting requirements. One of these is a minimal migration of the centre of pressure over the normal range of operating conditions so that excessive feathering couples are not fed back into the controls.

In a cambered airfoil, the centre of pressure moves fore and aft with changes in angle of attack. The downward twist at high speed was enough to twist the blades against the pilot’s efforts on early machines and caused some crashes. For some time, helicopters used little or no camber in the blade section, but subsequently cambered sections having reflex trailing edges were developed which reduced the centre of pressure move­ment. This along with the development of structures with greater torsional stiffness allowed cambered blades to return to use, although almost invariably in conjunction with powered controls.

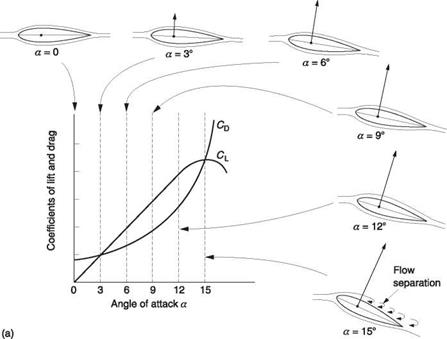
Lift is equal to the rate of change of momentum induced downwards into the sur­rounding air. For unit airfoil area, it is proportional to the air density, the square of the relative air velocity and, as was seen in section 3.1, it is a function of the angle of attack. When an airfoil section is tested, the reaction is resolved into horizontal and vertical directions with respect to RAF so that two factors of proportional­ity, called the coefficient of lift CL and the coefficient of drag CD are measured. Figure 3.5(a) shows how these coefficients change as a function of the angle of attack. For small angles CL is proportional as it was seen in Figure 3.1(c) that the accel­eration of the airflow is proportional to the angle through which it is deflected. As the angle of attack increases the reaction rotates back and the lift component of the reaction will be smaller than the reaction. The graph curves away from pro­portionality. At a large angle of attack, separation takes place, and the CL drops sharply, accompanied by a sharp increase in CD. When this occurs the airfoil is said to be stalled.

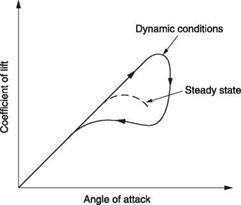
An airfoil does not stall immediately the angle of attack is raised, and if the rate of angular change is sufficiently high the lift momentarily available might be double the amount available in steady-state conditions. This is variously called the Warren effect or dynamic overshoot and is shown in Figure 3.5(b). In the case of a helicopter the angle of attack is changing at rotor speed and dynamic overshoot has a considerable effect. In practice it means that helicopter rotors may not lose significant amounts of lift through stall.

In this respect the helicopter has the advantage over the fixed-wing aircraft. The latter has to be flown at all times with the probability of a stall in mind. Even when the pilot has sufficient airspeed, a sudden gust due to wind shear or a microburst can reduce that airspeed and cause a stall. It was this concern that led Juan de la Cierva to develop the gyroplane. He correctly argued that a rotary wing aircraft that could not stall would be safer.

The coefficient of lift cannot be controlled directly; in order to obtain a certain CL the airfoil must be set to the appropriate angle of attack. The drag is also a function of angle of attack. It is more useful to know the ratio of lift to drag, since the peak value of this, L/Dmax., indicates the most efficient mode in which the airfoil can be used.

Fig. 3.5 (a) How lift and drag change with angle of attack. Initially lift is almost proportional whereas drag changes with the trend shown. As there is profile drag at all angles of attack, the curve does not start from zero. The most efficient use of the airfoil will be where the l/d ratio is greatest. At steady large angles of attack the airfoil stalls. (b) Stall does not occur instantaneously and for a short time after a large angle of attack is applied, lift increases. With their rapidly feathering blades, helicopters can exploit this phenomenon.

For a given engine power, the greatest lift in the hover would be obtained by operating the blades at the maximum lift over drag ratio. However, a practical helicopter cannot operate in this condition because it would be unsafe in forward flight. Many manoeu­vres, such as a banked turn, require the rotor to produce a thrust which exceeds the static weight of the machine. The ratio of thrust to static weight is called the load factor.

A rotor hovering at L/Dmax. has a load factor of unity and would stall in any real manoeuvre. It is thus a characteristic of helicopters that the rotor must operate below L/Dmax. of the blade section in the hover in order to allow a reasonable load factor for forward flight.

Turning at a given rate (number of degrees per second) requires a lateral acceleration proportional to the square of the airspeed. As aeroplanes tend to fly faster than heli­copters, they will need high load factors to obtain reasonable rates of turn. Aeroplanes automatically have high load factors at speed because available lift increases as the square of the airspeed. In helicopters lift is dominated by rotor speed, not airspeed and so load factors in helicopters tend to be small although helicopters can still easily out-turn most aeroplanes.

As the relative airflow in helicopters is dominated by the rotor speed, the gust response of helicopters is much reduced in comparison to that of aeroplanes. This is one reason why helicopters can operate in bad weather. A further small luxury is that the flexibility of the rotor gives in gusts a decoupling effect similar to that given by the suspension of a car.

In a hovering helicopter, the only source of lift is the rotor. Obtaining sufficient lift is only a matter of providing a suitable combination of power and efficiency, and is much easier than controlling lift. As the lift is proportional to the square of the speed, it is in principle possible to control lift by changing the rotor speed. Some early machines did just that. Unfortunately, the inertia of the rotor means that speed changes cannot rapidly be accomplished. For practical reasons a constant rotor speed is much to be preferred.

The proportionality between the coefficient of lift and the angle of attack is the solution. As was shown in Figure 3.1, the rotor blades are mounted on feathering bearings. Figure 1.21 showed that the pilot holds in his left hand a collective pitch lever pivoted near the back of his seat. The lever gets its name because by lifting it, the pitch angle of all of the rotor blades is increased by the same amount, and the rotor lift increases immediately. This feature of the helicopter contributes enormously to its safety. When a fixed-wing aircraft flies slowly, sudden loss of lift can only be countered by raising the airspeed and this takes time. In the helicopter the airspeed is always present due to the rotating blades and as this speed is many times higher than any normal windspeed, the airspeed seen by the blades is always adequate.

In addition to instantaneous response to changing lift conditions, the helicopter rotor stores in kinetic energy the equivalent of full engine power applied for several seconds. The pilot can transiently increase the available power by using so much collective pitch that the rotor slows down and converts its kinetic energy into lift.

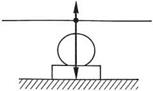
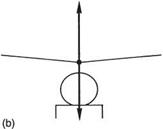
Figure 3.6(a) shows a helicopter with flight RRPM, but with the collective lever lowered. The thrust vector is small, so gravity keeps the machine firmly on the ground. If the collective lever is raised, eventually the rotor thrust vector will exceed the weight, and the machine will rise. By adjusting the collective lever, the machine can be made to hover with the thrust exactly balancing the weight as in (b). If the thrust is directly

upwards, there is no resultant and the machine stays still. In the still-air hover, the inflow through the rotor is axial, and if, for simplicity, it is assumed that the centre of gravity of the machine is at the mast, the forces on the blades will not vary as they turn.

The collective control can be used to make the rotor thrust greater than or less than the weight of the machine. The force imbalance causes the machine to accelerate up or down. However, this acceleration does not continue indefinitely. Figure 3.7(a) shows that as the machine rises, the angle of relative airflow experienced by the blades is

Fig. 3.6 (a) With the collective lever lowered, the rotor thrust is less than the weight and the machine remains on the ground. (b) With an appropriate setting of the collective lever, the rotor thrust can be made exactly equal to the weight.

Actual direction of blade through the air

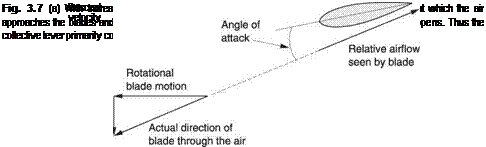
Rotational blade motion

(b) Descent

reduced by the vertical velocity. This tends to reduce the angle of attack and hence the rotor thrust. As a result the vertical velocity reaches a value where the rotor thrust once more balances the weight and the velocity then remains constant.

Figure 3.7(b) shows that if the collective control is lowered, the machine accelerates downwards, but the change in relative airflow is such that the rotor thrust is increased. The vertical velocity again stabilizes at a value where the thrust balances the weight. Thus the effect of the collective control in the hover is primarily to control the vertical velocity.

In most powered flight conditions, but particularly when hovering, the rotor is work­ing in the descending airflow it has itself caused. This self-inflicted problem is called inflow. When inflow is present, there is a vertical component of airflow vectorially to be added to the local blade velocity in order to find the direction of the RAF.

The pilot controls the pitch angle using the collective lever and this, along with the velocity of inflow through the rotor, determines the angle of attack. As a result there is no one correct position for the collective pitch lever and the pilot will need constantly to adapt the collective pitch setting for changes in speed, fuel burned and altitude. As there is no correct position for the collective lever, there is no spring centring. Instead there may be a friction mechanism that can be adjusted to hold the lever at the last position without unduly adding to the force needed to move it. This allows the pilot to release the lever for short periods in order to operate secondary controls.

In a helicopter having a hingeless rotor, the displacement between the area where lift is generated and the hub where the load is applied causes upward bending stresses that increase dramatically towards the rotor head. The underside of the blade is placed in tension, and the upper surface is placed in compression. The rotation of the blades produces a tension along their length that also increases towards the rotor head. The stress caused by this tension is of the same order as the stresses due to bending, and the stress on the underside of the blade is roughly doubled, although the compression on the upper surface is relieved. The drag of the blades causes a rearward bending stress that is constant in the hover.

There is a tendency for the blade rotation to force the blade to twist to a pitch angle of zero. Figure 3.8(a) shows that when the blade is set to zero pitch, the leading and trailing edges of the blade are further from the feathering axis than when pitch is applied. In order to set the blades to a working pitch, some of the mass of the blade must be brought closer to the shaft axis, and work will need to be done against the rotational forces that will be reflected as a reaction seen by the control system.

The effect can be reduced by the use of so-called Chinese weights that are placed on a rod at right angles to the chord line as shown in Figure 3.8(b). These will tend to move away from the rotor shaft axis as a result of rotation. The term comes from the tales told by sailors to the gullible alleging the orthogonality of certain parts of the anatomy of the oriental female at a time long before the development of either the helicopter or political correctness.

A less colourful alternative is to incorporate a spring into the collective linkage that is adjusted to supply a steady force to hold the blades at a typical positive pitch, relieving the pilot of the need to apply a constant force to the collective lever. When the blades are not turning this spring may be powerful enough to force the blades to maximum pitch and so the collective lever is fitted with a lock that the pilot can apply prior to shutting

(b)

down the rotor. Another possibility is for the rotor head to incorporate centrifugal weights that only apply an upload to the collective when the rotor is turning.

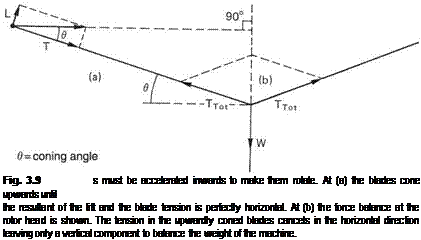
Anyone who has examined a parked helicopter will immediately notice how droopy the blades are. A considerable deflection can be obtained by lifting the tip with one finger. How, then, can the blades lift the weight of the helicopter? The answer is that the rapid rotation in conjunction with the mass of the blades causes them to be pulled out straight; a phenomenon called centrifugal stiffening. Rotating blades are not in static equilibrium and they must be made to accelerate towards the shaft if they are to follow a circular path, and this requires a considerable inward or centripetal force, which will always be an order of magnitude more than the weight of the helicopter.

Figure 3.9(a) shows that if the blade bends upwards, the downward component of the centripetal force will balance the lift at some coning angle, and the resultant will be a horizontal force only so no further bending takes place. The reaction of the blades at the rotor head is shown in Figure 3.9(b). The force from the coning blade has an upward component, which is the lift, and an outward component due to the rotation.

In the hover, if the blades are properly balanced and all have the same coning angle, the horizontal forces cancel in the rotor head and only lift results. Adjusting all of the blades to the same angle is achieved using the process of tracking which ensures that the collective control applies exactly the same pitch to each blade. Clearly, if the blades

are not balanced or not tracking, vibration will result. Accurate blade balancing and tracking is important and the necessary techniques will be considered in section 4.19.

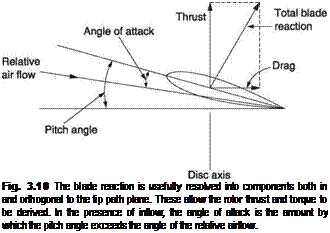
Whilst resolving the airfoil reaction into lift and drag is useful for fixed wings, it is less useful for helicopters because of the feathering action of the blades. Figure 3.10 shows how the reaction on a rotor blade can be resolved in a more useful fashion. As the only real force on the airfoil is the reaction, resolving the force into components is only taking place in our imagination, so we can resolve into whatever directions we find useful. In helicopters, whatever the mechanical pitch angle of the blade, and whatever angle of attack results, it is more convenient if the reaction is resolved into the rotor thrust acting substantially at right angles to the tip path plane or rotor disc, and the rotor drag acting in the tip path plane.

The angle of attack is the angle by which the pitch angle exceeds the angle of the RAF. The reaction of the airfoil is tilted further back in the presence of inflow, so that a larger component of the reaction is opposing the thrust delivered by the engine, and power is consumed simply driving against it. The rotor thrust is also slightly reduced by the tilt of the reaction. The hover out of ground effect (HOGE) is a particularly power consuming exercise. Inflow tilts back the blade reaction to oppose the engine, so that more torque is required to drive the rotor and more tail rotor power will be needed to balance the torque. HOGE is also one of the worst situations in which to lose power as the high rotor drag will reduce RRPM more before the pilot reacts and lowers the collective lever.

Clearly increasing the collective pitch will increase the induced drag, and so more power will be required to maintain rotor speed. In simple piston engine helicopters, the end of the collective lever is fitted with a twist-grip connected to the throttle. Main­taining RRPM is then the responsibility of the pilot who will need to monitor the rev. counter. In more sophisticated piston engine machines and in all turbine machines automatic rotor speed governing systems or throttle correlators are used. The pilot

just changes the collective pitch and the system computes the engine power for itself. Correlators will be described in Chapter 6.

Without considering constructional details, it is possible to conceive of an ideal hover­ing rotor as an actuator disc that somehow accelerates air downwards over a circular region and develops thrust from the reaction. In this case the operation of an ideal rotor can be analysed theoretically from the change of momentum of the air passing through. The concept of an ideal rotor is useful because it can act as a benchmark with which to compare real designs. Clearly the performance of the ideal rotor can only be approached, but never exceeded.

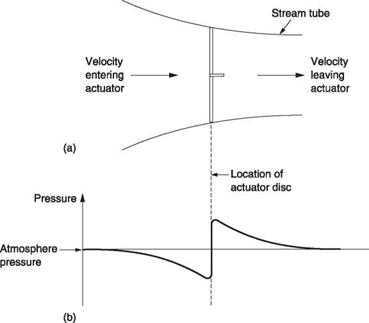
Figure 3.11(a) shows the actuator concept which makes some simplifying assump­tions. One of these is that the air is somehow constrained to flow only within the tapering column shown, known as a stream tube, and doesn’t mix with the surrounding air. The mass of air passing any horizontal plane in the column per unit time must be constant. The actuator causes a pressure difference to exist across itself. This pressure must be given by the thrust divided by the disc area. A further assumption is that this pressure is uniform. The pressure difference across the actuator can only be sustained locally. Figure 3.11(b) shows that at a distance, the pressure must be the same as static pressure. To allow the pressure difference across the actuator, the pressure must have a falling gradient along the streamlines except at the actuator itself.

Bernouilli’s theorem can be used to predict what happens along a stream tube. Bernouilli’s theorem is simply another example of conservation of energy. Air has a static pressure and a dynamic pressure due to its motion. Bernouilli’s theorem states that the sum of the two, known as the head, remains constant. As a result when static pressure falls, the dynamic pressure must increase to compensate. As the density doesn’t change significantly, the velocity must increase. Clearly Bernouilli’s theorem does not hold across the actuator, as energy is put into the air there.

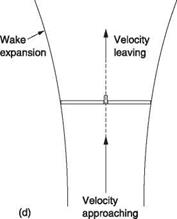
Except for the pressure step at the actuator, the air in the stream tube experiences a falling pressure gradient which causes the stream to accelerate and contract. This is the phenomenon of wake contraction seen in propellers and rotors. Thus the velocity with

Fig. 3.11 (a) In actuator theory, air passes along a stream tube which is intersected by the actuator. (b) In order to allow a step pressure difference across the rotor, pressure must fall both approaching and leaving. Note the wake contraction to about 0.7 of the rotor diameter.

which air arrives at the actuator is higher than it is some distance before the actuator. This difference is the induced velocity. The induced velocity is important because it determines the velocity the rotor sees which has a large bearing on the RAF and the power needed. It should not be confused with the final velocity which is higher still.

In the case of an actuator that is climbing vertically, the rotor thrust is given by the rate of change of momentum of the air passing through the disc. The power needed must be the product of the thrust and the velocity, where the velocity is the rate of climb plus the induced velocity. This power must be equal to the difference in the kinetic energy well above and well below the disc. Clearly this assumption implies that only the induced drag is being considered. Actuator theory cannot account for profile drag and assumes it to be zero.

The increased velocity applied to the downwash is twice the induced velocity at the disc. In a stationary hover, the total velocity is the induced velocity alone and the downstream velocity will be twice this. In practice the contraction has completed by about one diameter below the rotor. At this point, as the velocity has doubled, the cross-sectional area must have halved in order to have constant mass flow and so the downwash diameter will be about 0.7 of the rotor diameter.

In Figure 3.11, uniform inflow over the disc is assumed. In other words the induced velocity and the pressure are the same all over. This is the most efficient condition. It is easy to show that any other condition requires more power. For a given total thrust, if one area of the disc has greater induced velocity and thrust, another area must have less induced velocity and thrust. The thrust is proportional to the momentum change, which is in turn proportional to the induced velocity, whereas the kinetic energy imparted is
proportional to the square of the induced velocity. Thus the power saved in an area of reduced thrust does not compensate for the extra power needed in an area of increased thrust because of the square law. It follows that the minimum power is required when the thrust per unit area is constant.

Helicopter flight is dependent on a pressure difference across the rotor disc that disturbs the air. Such pressure disturbances travel at the speed of sound and can thus easily travel long distances from the helicopter. It should be clear that a helicopter in flight is associated with the induced movement of a significant air mass. Such a moving mass cannot change its velocity in an instant. Consequently a rapid change of blade pitch does not result in an immediate change of inflow velocity. This will result in an angle of attack initially higher than in the steady state and this may result in a thrust overshoot. The same effect is observed in sailing vessels where there is a lag between sheeting the sails and a change in sail reaction. The phenomenon is known as dynamic inflow and is a macroscopic version of the dynamic overshoot phenomenon of Figure 3.5. The inertia of the associated air mass will also have effects in translational flight as will be seen in section 3.21.

The actuator concept is useful, but it does not consider a number of real world factors, not least profile drag. Blade element theory takes this into account and allows a more accurate result to be obtained. In the hover the forward speed of some point on a blade is proportional to the radius of that point. It is possible to analyse the performance of a rotor by considering it to be made of small elements where the conditions over each element are substantially constant. The overall result is obtained by adding up the contribution from each element.

At each blade element, the inflow must be known so that the RAF and the effective airspeed can be calculated. The characteristics of the blade section employed at that element must be consulted to find the resultant aerodynamic force on the element that will be resolved into an element of rotor thrust and an element of drag. All of the axial thrusts from the elements can simply be added to find the total thrust. The drag of each element is multiplied by the radius of the element concerned to obtain an element of rotor torque. These elements are then added to obtain the total rotor torque.

Blade element analysis is only as accurate as the assumptions made about the inflow. Actuator theory gives some idea about the inflow, but in a real rotor the inflow at the tips and the blade roots will be non-ideal. More accurate results require the use of vortex theory to take into consideration the conditions at the blade root and tip.

The thrust production mechanism in the helicopter creates a pressure difference, which causes the air to accelerate downwards. To maintain height, the rotor then has to climb up through the air at the same speed as the air is coming down. Work is being done on the air and the power is the product of the weight of the helicopter and the induced velocity. It follows that the power needed to hover can be minimized by reducing the induced velocity. This can be achieved by reducing the disc loading. This is the helicopter’s equivalent of span loading in a fixed-wing aircraft. Where power is limited, as in piston engine helicopters, a low disc loading will be needed to extract more lift

from the available power. Some of that lift will be lost because the larger rotor will be heavier.

In a turbine helicopter, the engine and fuel supply weigh less for the power the engine produces and so a better result may be obtained by using a smaller rotor and transmission that also weighs less to obtain a greater useful payload. A comparison of, for example, an Enstrom F-28 and a Hughes 500 illustrates this point.

This cannot be taken to extremes, as there is a practical limit to the downwash velocity. This is reached when objects on the ground are blown about and become a hazard. The CH-53E Stallion represents about the limit of acceptable downwash velocity as it is almost impossible to stand in the downwash. A further consideration is that in autorotation a machine with a high disc loading may have a rapid rate of descent, leaving the pilot little margin for error in judging the flare-out in the case of an engine failure. On the other hand a machine with a low disc loading may have very good autorotation performance, the Enstrom being a particularly good glider.

Once a disc area and loading has been decided, some consideration has to be given to the tip speed. Profile power is proportional to the cube of the tip speed, whereas thrust is proportional to the square of the tip speed. The minimum profile power is where the minimum possible tip speed is used to operate the blades at L/Dmax., which will be just below the stall. Reducing the tip speed will require the blade area to be increased to maintain thrust. Consequently the disc area is chosen to give the desired disc loading, whereas the blade area is chosen to produce sufficient rotor thrust (with an adequate load factor) at the chosen RPM. The ratio of the total blade area to the disc area is known as the solidity. Although low tip speeds and high solidity reduce profile drag and improve hovering performance, a machine built to these criteria would not have an adequate load factor for forward flight. It will be seen in section 3.24 that a low tip speed is also detrimental to forward flight as well as being a liability in the case of a power failure as the rotor stores little energy, giving the pilot little time to react and establish autorotation.

In a conventional helicopter there will always be a compromise between hover and forward flight performance. Possible technical solutions include variable rotor speed and variable diameter rotors.

In the hover a low rotor speed would reduce profile drag by allowing the blades to operate closer to L/Dmax., whereas in cruise a high rotor speed would improve the load factor. To obtain maximum power from a piston engine at both speeds, a two – speed transmission would be needed, and there would be some weight and cost penalty. Changing the speed would be easy with a free turbine engine. There would also be a problem in detuning the rotor to minimize vibration at two different speeds. These problems are not insuperable.

A variable diameter rotor could have a low disc loading for efficient hover, but a raised disc loading in cruising flight. The technical problems here are enormous but may one day be economically viable.

Whatever the disc loading, in a constant height hover, the potential and kinetic energy of the helicopter remain constant, and so no work is being done on the helicopter. Thus the mechanical efficiency of all helicopters in the hover is zero. Clearly mechanical efficiency is not a useful metric, because it doesn’t allow comparison. A better metric is to compare the power theoretically needed by an ideal actuator with the actual power

needed in the real helicopter where the actuator has the same diameter as the rotor. This is the origin of the figure of merit.

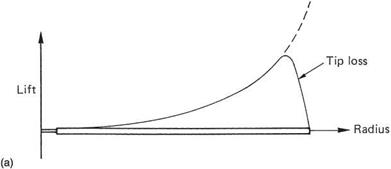
The forward velocity of the rotating blade increases linearly from zero at the shaft to a maximum at the tip. This is not a good starting point from which to obtain uniform inflow, but the rotor is the only practical approximation to an actuator disc that anyone has devised. The figure of merit may be improved by twisting and tapering the rotor blades. Figure 3.12(a) shows that in untwisted, untapered blades, the lift will be produced increasingly toward the tips as a parabolic function, until tip loss dominates.

Given the induced velocity is required to be uniform, it is easy to calculate the pitch required at any radius to make the angle of attack constant along the blade so that the whole blade operates at an efficient L/D ratio. However, in practice the induced velocity will be a function of radius and such a twist will not be optimal. Twist that takes account of induced velocity distribution is known as ideal twist. In fact ideal twist is academic because the amount of twist would have to change as a function of induced velocity and clearly it does not in any practical blade.

Ideal twist does not achieve uniform inflow, because of the reduced effectiveness of the inner slow-moving parts of the blade. Tapering the blade as well as twisting it removes area at the fast moving tips and places it in the slower moving areas where induced velocity is ordinarily lower. Ideally, the rotor chord needs to be inversely proportional to the radius. This results in an impractical rotor for a helicopter, but the technique

Fig. 3.12 (a) An untwisted, untapered blade has a parabolic lift distribution and far from uniform inflow. (b) Taper and twist improve the uniformity of inflow.

will be found in axial blowers where the root chord may be several times the tip chord. Figure 3.12(b) shows a better lift distribution resulting from a combination of twist and taper. Blade taper has the further advantage that the various vibration modes of the blade will not be harmonically related. This will be considered in section 3.26.

In practical helicopters the blades cannot extend all the way to the mast because of the need to provide a rotor head mechanism. A further consideration is that, in the hover, the extreme roots of the blades simply provide a downwash onto the hull resulting in a download, negating some of the rotor lift. Section 3.20 will show that, in forward flight, the blade root of the retreating blade encounters reverse airflow. As a result blades often have a significant root cut. Ideal twist for hovering will not be ideal for forward flight or autorotation and a compromise is invariably necessary. In the proprotors of a tilt-rotor helicopter more twist will be possible because the rotors work with predominantly axial flow.

In a real rotor, the downwash does not just move downwards, but it also has a rotational component of motion known as swirl. Intuitively it is clear that the turning rotor must turn the air with it to some extent. Figure 3.10 showed that the reaction on a lifting blade is somewhat aft of the rotor shaft axis. It must follow that the direction in which the momentum of the inflow increases is in the opposite direction. The vertical component is the inflow velocity, which produces lift, whereas the horizontal component creates swirl which represents wasted power.

Some of the swirl is due to profile drag and some is due to induced drag. In the absence of profile drag, the blade reaction is still slightly behind the vertical and this must result in a small loss when compared with an ideal actuator that only causes vertical inflow. The main source of swirl is the result of profile drag adding to the rotational momentum of the air. In an ideal actuator the air leaves with increased vertical momentum only. In a real rotor the amount of swirl gives an indication of the figure of merit. The higher this is, the lower the swirl will be. In a twisted blade, swirl will be greatest near the root where the pitch angle is greater.

The torque delivered to the rotor shaft can be divided into two parts, first the torque needed to drive an ideal rotor which only produces an increase in vertical momentum sufficient to create the required thrust, and second an additional torque which is the reaction to creating swirl and tip vortices. With a single rotor, swirl energy is lost forever, but in contra-rotating rotors, the swirl of the second rotor can cancel the swirl of the first. Unfortunately this does not reduce profile drag, it only reduces induced drag.

In the single rotor helicopter, the main effect of swirl is that the downwash on the hull is not vertical, which adds to the general air of asymmetry surrounding the helicopter. The effects will be considered in Chapter 5.

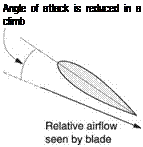
The direction of the reaction on an airfoil depends upon the angle of attack. When hovering, inflow causes the resultant to be tilted back and opposes the engine thrust. If, at a suitable height the collective pitch is lowered, the machine starts to fall, the inflow reverses and the relative airflow has an upward component. Figure 3.13(a) shows that the principle of the rotor blade in autorotation is no different to powered flight. It continues to accelerate air into a new direction. However, as the air approaches

Fig. 3.13 In autorotation, inflow is reversed. Air approaches from below so that the reaction has a forward component. (a) Middle part of blade is driving, taking momentum from the air. These conditions can be obtained with positive blade pitch. (b) Outer part of blade has a lower angle of attack and is being driven as in normal flight. (c) Inner part of blade has high angle of attack and is stalled. (d) The rotor takes momentum from the air and so the wake is slower than the approaching air and expands. This should be compared with Figure 3.11.

upwards, the acceleration has a rearward component. The reaction to this is forward, so the rotor can be driven against profile drag and transmission losses. At a suitable setting of the collective pitch, the overall reaction on the blades is brought to the vertical and so they will continue to turn at the same speed and provide lift. Note that in order to produce lift the blade must have a positive angle of attack with respect to RAF and so it is common for the blade to have positive pitch in autorotation.

The machine is moving steadily downwards using potential energy to overcome pro­file drag. In fact the rotor is taking momentum from the air so that induced power becomes negative and provides the profile power needed. The strict definition of auto­rotation is the requirement for zero shaft torque. Where a rotor actually delivers shaft power it is said to be windmilling or in the windmill brake state. A real helicopter in autorotation is technically windmilling because the shaft torque is not zero. In the absence of the engine, some shaft torque is needed to turn the tail rotor and any other important items such as hydraulic pumps.

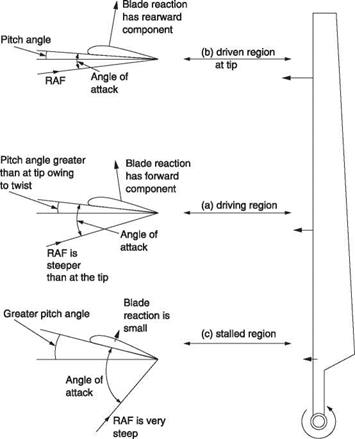
The speed of a blade element is proportional to radius. A further complication is that most rotor blades have twist to improve the hover figure of merit, but in autorotation the inflow is reversed and the twist is the opposite of what is needed. It can be seen that on moving from tip to hub, the RAF decreases in speed but the angle of attack increases. As a result the central part of the blade, shown at Figure 3.13(a) is being driven by the inflow and is windmilling. Figure 3.13(b) shows that the tips have a small angle of attack and high airspeed. Profile drag dominates and L/D is poor, with the total blade reaction being behind the vertical. This area of the blade is producing lift and induced drag as if it was in the power-on condition. Figure 3.13(c) shows that the innermost parts of the blades are stalled as they have a high angle of attack and a low airspeed. The power needed to drive the tips and the inner parts of the blade comes from the windmilling of the centre parts. Only a small section of each blade at the boundary between the driven and driving regions is technically autorotating with a vertical total blade reaction. Thus what is meant in practice by autorotation is that the entire rotor has zero net torque. The entire rotor can also be considered to have an L/D ratio and in autorotation the slowest rate of descent will be where this is used.

In practice the loss of performance in autorotation due to twisted blades is surpris­ingly small. One reason for this is that the profile drag is determined only by the rotor speed and is largely unaffected by local angle of attack. Another is that real blades don’t have anything like ideal taper and also have root cut-out so the stalled inner part of the rotor doesn’t absorb as much power as might be expected.

In autorotation there is still a pressure step across the rotor, but the inflow is now from below. Figure 3.13(d) shows that as the rotor is taking momentum from the air, the slipstream from the rotor is slower than the inflow. The pressure gradient along a streamline is rising and so the wake expands.

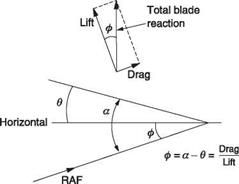
In autorotation the best rate of descent will be where the entire rotor (not a blade section) operates at L/Dmax.. The highest RRPM will also be obtained at L/Dmax., giv­ing the greatest stored energy for landing. Figure 3.14 shows an autorotation diagram in which the vertical axis is drag over lift and the horizontal axis is angle of attack a. It will be seen from the figure that, at an idealized blade radius, the ratio of drag to lift determines the angle p which must also be the angle of RAF if the blade reaction is to be vertical. If the pitch angle is в, then p = a — в. The function a — в is shown on the graph to be a straight sloping line. The lowest profile drag will be at the bottom of the drag ‘bucket’ and the pitch angle to achieve that is where the line of a — в intersects the a axis. Most conventional helicopters will be rigged so that the minimum pitch stop on the collective lever is at about this value. Thus operation in autorotation is in the region to the right of the intersection, but not so far as the position of the dotted line where rotor

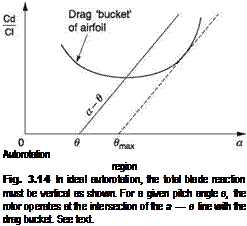speed may be irrevocably lost. In this region rotor speed may be changed by alteration of the balance of forces. Reducing the angle of attack causes the blade reaction to move forward from the vertical. Negative induced power exceeds the profile power require­ment until the rotor speed has increased. On the other hand, increasing the angle of attack causes the reaction to move behind the vertical, and the rotor speed falls.

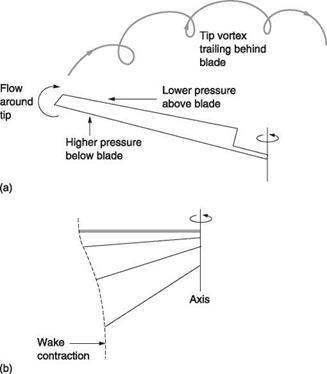
The pressure differential between the upper and lower surface of the rotor disc causes air to try to flow transversely around the tip in order to equalize the pressure. This rotary flow combines with the blade velocity to leave a corkscrew-like trail shown in Figure 3.15(a) and known as a vortex. The loss of pressure differential due to this vortex generation cancels out the lift generated at the blade tip; an effect known as tip loss. Nearly 10% of the blade length is useless. The power needed to overcome induced drag at the tip is wasted generating the vortex. There must also be a vortex at the inboard end of the blade but it is less powerful because the lift gradient is much lower. In the steady hover and in forward flight, the tip vortices are swept away downwards by inflow.

Fig. 3.15 (a) The pressure difference across the blade due to the generation of lift results in a flow from bottom to top around the tip that results in a spiral vortex. (b) In the hover the tip vortices are swept away downwards, but not as fast as the inflow which is generally faster towards the tip.

Tip loss may be reduced by tapering and by twisting the blade near the tip so that the angle of attack is small. The pressure differential is then minimized across the tip. This cannot be taken too far as very small tip chords will operate at poor Reynolds numbers and suffer poor L/D. As a practical matter space will also be needed for tip weights.

It will be seen in Figure 3.15(b) that the result of non-uniform inflow is that the air disturbed by the passage of the blades changes from a disc to a cone and shrinks in diameter due to wake contraction.

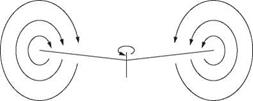
In autorotation the vortices are swept away upwards. Thus in climb, hover or auto­rotation the vortices are always carried off by the slipstream. However, if a vertical pow­ered descent is attempted, the machine descends into its own inflow and the vortices from successive blade sweeps are closer together and begin to reinforce one another. As the vertical rate of descent approaches the induced velocity, the vortices will not be swept away so much, and will begin to augment one another. The airflow will recircu­late, in a toroidal motion known as a vortex ring. This is shown in Figure 3.16. The recirculation is increasing the inflow and so more collective pitch is needed to provide the same lift. The blade reaction will tilt back and more torque will be needed.

Paradoxically, a helicopter needs more power to descend in the hover than it does to maintain height. Early helicopters having marginal power used low disc loading

Fig. 3.16 When the helicopter descends vertically, it can catch up with its own wake and the rotor vortices are not swept away, but result in recirculation. If allowed to develop fully, the result is the vortex ring condition.

Fig. 3.17 The relationship between induced velocity and vertical climb/descent velocity. Both have been normalized with respect to induced velocity in the hover. Note there is a discontinuity between powered descent and autorotation due to the vortex ring condition.

and so had low induced velocity. Some suffered from power settling where above a certain rate of vertical descent the descent could not be arrested except by moving into forward flight.

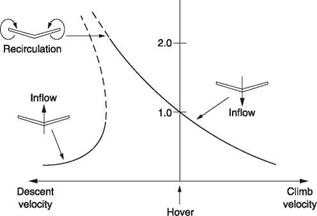
Figure 3.17 shows the relationship between the induced velocity needed and the climb/descent velocity. As the effects are proportional to the hover induced velocity, Figure 3.17 has been normalized by dividing both parameters by that factor. As a result the curve passes through unity in the stationary hover. Note that as the rate of descent increases, following the curve to the left, there is a discontinuity where a fully developed vortex ring condition occurs. The recirculation has now enveloped the rotor whose ability to produce lift is considerably reduced. The effectiveness of the cyclic pitch will also be reduced. Increasing collective makes it worse. The machine drops like a stone, pitching and rolling randomly. If this condition is entered close to the ground, recovery may be impossible.

To create lift a rotor must have mass flow whose momentum it can increase. In hover or climb, the inflow is downward and the rotor puts momentum into the inflow by accelerating it. In a vertical autorotation the inflow is upward (effectively making the momentum negative) and the rotor puts momentum into the air by slowing it down. Both of these conditions are stable and the results are predictable from actuator disc

theory. The problem is that in vertical flight to get from downward inflow to upward inflow the state of zero inflow must be traversed.

Zero inflow makes nonsense of actuator disc theory, and the real helicopter can’t fly in that condition either, hence the discontinuity in the curve of Figure 3.17. The position of the discontinuity is affected by blade twist. A twisted blade produces more thrust at the inner parts of the disc and excites the vortex ring less, so it is possible to descend faster.

It must be accepted that there are certain combinations of vertical rate of descent and induced velocity in which a helicopter will be uncontrollable. Thus an important part of pilot training is to impart a practical knowledge of how to fly outside that region, how to recognize the onset of a vortex ring and how to recover from it.

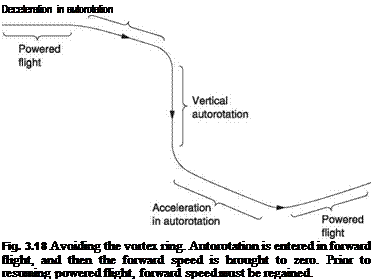
Using forward speed to guarantee an inflow allows the vortex ring condition to be avoided. Figure 3.18 shows that to enter autorotation from forward flight the collective is simply lowered until the inflow reverses. Once in autorotation the forward speed can be brought to zero for a vertical descent. In order to terminate the vertical autorota­tion forward speed is regained before raising collective pitch again to obtain normal downward inflow.

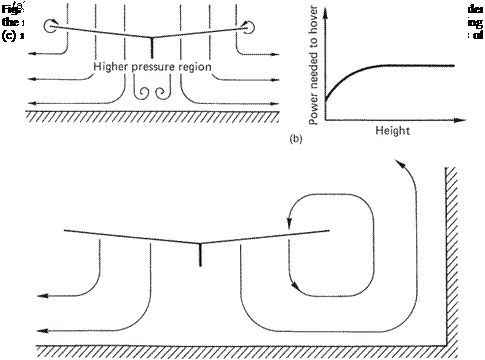
When hovering close to the ground, the air passing downward through the rotor cannot escape as freely as shown in Figure 3.19(a). Air pressure below the machine builds up, and reduces the induced velocity. The RAF is closer to the horizontal and the blade resultant is closer to the vertical. The same lift can be obtained from the rotor with less rotor drag. As Figure 3.19(b) shows, considerably less power is needed to hover close to the ground. As the figure shows, ground effect is noticeable up to a height approximately equal to the rotor radius. In still air, a helicopter will reach equilibrium in ground effect at a height where the lift just balances the weight without any input to the collective pitch

control. If the machine descends, it will obtain more lift from the air cushion; if it climbs, the lift will fall. In many respects the helicopter in ground effect is like a hovercraft.

A helicopter in ground effect over water will displace some of its weight in a saucer­shaped depression in the water surface. This is not often seen because hovering low over water is a recipe for spray in the engines.

The presence of the rotor head and blade root cut-out creates a hole in the middle of the disc through which air can escape upwards in ground effect. This is actually another form of tip loss, which is called the fountain effect. In practice the fountain effect can be beneficial because it puts some of the hull into upflow and reduces the hull download. There will be vortices trailing from the inboard end of the blade. As the lift gradient is small here these are relatively weak and their main contribution is that in ground effect they make the hover conditions chaotic especially if they interact with the tail boom or tail rotor.

It is often stated by pilots that hovering over rough ground ‘dissipates’ the ground effect, when theory would suggest that restricting the ability of the downwash to escape would enhance ground effect. This aerodynamic effect ought to be very small, and the real effect may be psychological. When hovering over a crop, the pilot will estimate his height from the top of the crop, not from ground level. Thus the ground effect may not appear as powerful.

Ground effect normally increases lift so that it offsets the effect of vortex ring gener­ation. The two effects are always opposing one another. However, hovering close to a wall or next to another helicopter can trigger recirculation (Figure 3.19(c)).

In order to move around in the hover, the pilot pushes the cyclic stick in the direction he wants to go. This superimposes a cyclic variation of blade pitch on the average or collective setting. The result is that the blades oscillate sinusoidally about the feathering axis as shown in Figure 3.20(a) at the same frequency as the rotor turns. As a result the lift will increase on one side of the rotor and decrease on the other, resulting in a

One revolution

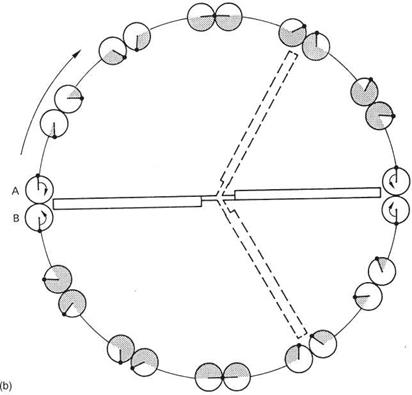
rolling couple. As was seen in Chapter 2, the rotor is gyroscopic and so the cyclic pitch change is arranged to occur 90° ahead of the required result to allow for precession in the rotor.

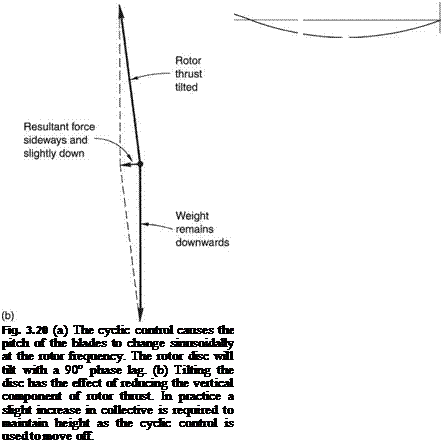
Figure 3.20(b) shows that the application of cyclic control tilts the thrust vector, and that there will be a resultant of the thrust vector and gravity which is primarily horizontal but also has a slightly downward component. This is because the vertical component of the rotor thrust becomes smaller when the disc is tilted. As a result the helicopter will accelerate sideways and lose height. To compensate, the pilot slightly raises the collective lever so that the vertical component of the thrust remains the same.

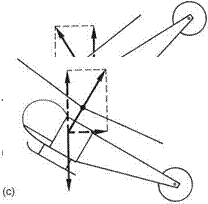
From the hover, the helicopter can be accelerated into translational flight by using cyclic pitch to tilt the disc. The greater the acceleration required, the more extreme will be the disc tilt and the greater the application of collective pitch. Figure 3.21(a) shows a helicopter at maximum horizontal acceleration. If done at low height, the blades can get very near the ground. Figure 3.21(b) shows that at constant speed and height the thrust necessary to balance the drag of the pure helicopter comes from the horizontal component of the inclined rotor thrust. The vertical component of the rotor thrust must balance the weight of the machine. Clearly the rotor thrust must be greater than in the hovering condition. The diagram simplifies the situation in that it assumes the drag of the fuselage acts at the rotor hub, which is not actually the case. In practice the drag acts below the hub to produce a couple which would depress the nose. There are two ways of dealing with that: using a rotor head which can apply an opposing couple from the blades and/or using a tail plane to produce a down thrust.

Note that the tip path plane may be inclined forwards with respect to the hull so that the balance of forces is obtained with the hull level. In this condition the drag will be minimized and the occupants will be most comfortable. A consequence is that when the machine comes to the hover it will sit with a tail down attitude. The length of the undercarriage legs or the angle of the skids is often arranged such that the machine can settle on the ground very nearly in this attitude.

Tilting the disc accelerates the machine along, but bringing the disc back to the horizontal only removes the acceleration, and the machine will continue along, slowing only because of drag. In order to stop, the disc must be tilted the opposite way to obtain acceleration in the opposite sense to reduce the velocity. Figure 3.21(c) shows a helicopter with maximum deceleration in a manoeuvre known as a quickstop. Note that the inflow has reversed so that a quickstop is actually a form of autorotation. Note that the tail boom is very low, and could strike the ground.

Figure 3.21(d) shows a turn at speed. The turn changes the direction but not the speed, so it is a change of velocity or acceleration. The acceleration must be towards the centre of the turn, and it is necessary to obtain a resultant sideways force to cause that acceleration. This is done by banking with lateral movement of the cyclic stick. Collective will need to be increased to maintain the vertical component of thrust equal to the weight. The machine will then fly around as if on the surface of a cone until the desired heading is reached, when the bank will be taken off and the collective reduced again. Note that in a 60° bank the thrust vector has to be twice that needed to hover in order to maintain height. The ratio of manoeuvre thrust to hover thrust is called the load factor. Not all machines can deliver that much power, and not all transmissions can accept it. However, some large transport helicopters can carry their

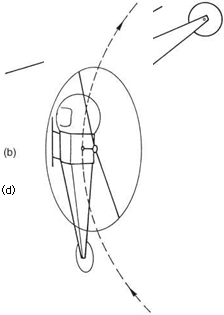Fig. 3.21 (a) The forces involved during maximum acceleration. Note the front of the disc can be very close to the ground. (b) The balance of forces in forward flight. The forward component of rotor thrust balances hull drag and the vertical component balances the weight. (c) The quickstop is a horizontal autorotation. Note the low position of the tail rotor. (d) A turn at speed is limited by the increased thrust necessary to maintain height whilst accelerating the machine towards the centre of the turn.

own weight in cargo. When unladen, their load factor effectively doubles and they can safely accomplish some quite alarming manoeuvres.

Note that during acceleration, deceleration and a correctly banked turn gravity still appears to act vertically down through the cockpit floor, and it is possible to complete an entire flight without spilling a mug of coffee placed on the floor.

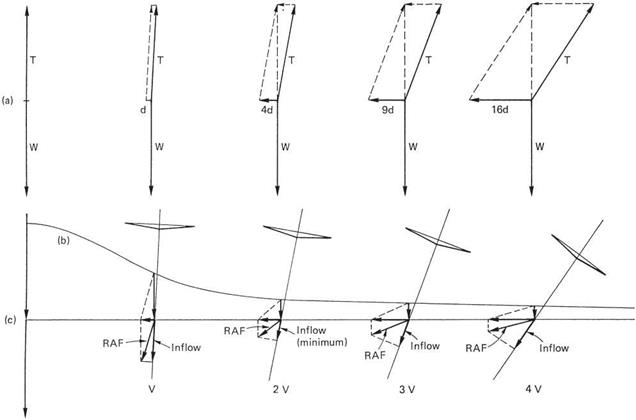
In translational flight, the forward velocity increases the velocity of the air passing the advancing blade and reduces that seen by the retreating blade. Figure 3.22 shows what happens. In (a) it can be seen that the velocity of a blade element due to rotation

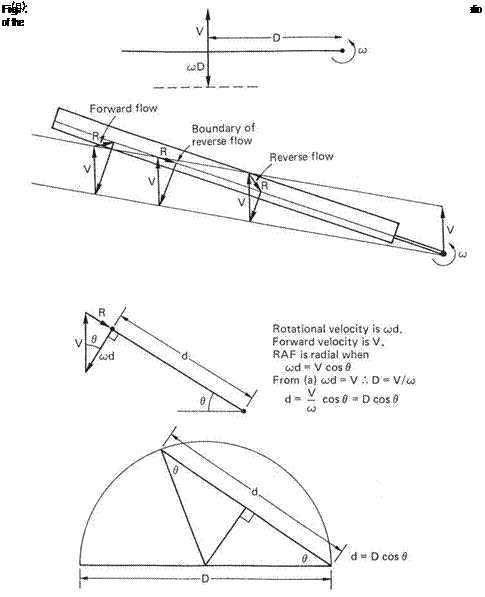is given by the distance D from the shaft multiplied by the angular speed w. When the blade is at 270°, the edge of the reverse flow region will be where wD equals the airspeed V. In (b) the method for finding what happens at an arbitrary blade angle is shown. At any distance d from the shaft, the vector resultant R of wd and V can be found. Figure 3.22(c) shows the derivation of the expression for d, the distance from the

shaft to the boundary of the reverse flow region. Figure 3.22(d) shows the expression for d graphically and it will be seen that the reverse flow area is circular and that its diameter increases with speed. Instantaneously the rotor is turning with respect to the outer edge of the reverse flow region. The ratio of forward speed to tip speed is known as the advance ratio г which is the same as the ratio of the diameter of the reverse flow region to the blade radius.

The retreating blade suffers reverse flow near the root; a small downward force may be experienced because the retreating blade effectively has a negative angle of attack due to flow reversal. Here is another reason for root cut-out, to reduce the amount of useless reverse-flowed blade. However, as the area is proportional to the square of the diameter, the amount of disc area lost to the reverse flow region is small. For example, at г = 0.4, the diameter of the reverse flow region is 0.2 of the rotor diameter but the area lost is only 4%.

Owing to the huge difference between the airspeeds, if nothing were done, the advanc­ing blade would produce more lift and the retreating blade less. This would apply to the rotor a roll couple toward the retreating side. The gyroscopic action of the rotor would result in a response delayed by 90° of rotation corresponding to a rearward pitch effect. This rearward couple is colloquially known as ‘flapback’ and it tends to reduce the forward tilt of the machine and consequently reduces the forward component of the rotor thrust, slowing the machine down.

Thus sustained forward flight requires a continuous application of forward cyclic control that reduces the angle of attack of the advancing blade and increases that of the retreating blade in order to balance the lift moments on the two sides of the rotor. In cruise the amount of cyclic pitch applied may be of the order of 5°. Flapback results in speed stability because it automatically opposes the cyclic control.

The more forward cyclic is applied, the higher will be the forward speed. Thus in translational flight the fore-and-aft position of the cyclic stick primarily controls the airspeed. If the airspeed is changed, the collective lever will need to be adjusted to maintain height because tilting the rotor thrust vector alters its vertical component.

In forward flight the rotor has access to a greater mass of air. Thus the same momen­tum increase and the same thrust can be obtained with a smaller induced velocity and this reduces the power needed. Figure 3.23 shows that there is a minimum induced power speed where the inflow velocity is the least.

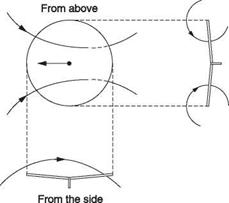
In flight, there is a region of low pressure above the rotor and a region of high pressure below. This pressure difference results in a tendency for air in the plane of the rotor to move upwards. Figure 3.24(a) shows that this happens for some distance from the edge of the disc. Simple inertia keeps the air moving upwards so that in translational flight, the leading edge of the disc encounters upwash. The upwash ceases when the downward impulse of the rotor cancels the upward momentum of the air mass.

In slow forward flight, Figure 3.24(b), the low pressure above the rotor has time to bend the inflow increasingly downwards as it reaches the trailing edge of the disc. The disc can be thought of as a low aspect ratio wing producing tip vortices which roll inward at the top and down through the rear of the disc. The result is a reduction of the angle of attack of the blade at the rear of the disc compared to that at the front. The loss of lift at the rear of the disc is subject to the phase lag, or precession, of the rotor and manifests itself as a roll to the advancing side, which is known as inflow roll.

Fig. 3 .23 Conditions for hover and four different airspeeds. In (a) note the drag d increasing as the square of the speed and requiring an increasingly forward tilt of the rotor thrust t. Curve (b) shows the vertical component of inflow. In conjunction with the airspeed this determines the direction and magnitude of the RAF (c). The actual inflow is the component of RAF along the rotor shaft. Note there will be a speed at which the minimum power is required to maintain height.

I Rising air in I the path of the I helicopter

(a)

(b)

(c)

Whilst coning causes no undue aerodynamic problems to a hovering helicopter, it has an unwanted effect in forward flight. Figure 3.24(c) shows that the effect of coning is to reduce the angle of attack of the blade passing across the tail compared with that of the blade passing across the nose. As for the inflow roll, this results in a tail – down moment applied to the disc, which likewise manifests itself as a roll towards the advancing side because of the phase lag of the rotor. The two effects take place in parallel, but as different functions of airspeed. Inflow roll commences on leaving the hover but reduces significantly as speed increases, whereas coning roll slightly increases

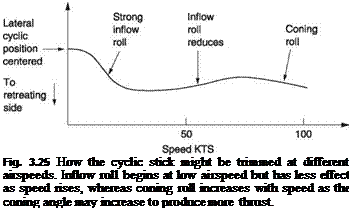
with airspeed. Figure 3.25 shows how the lateral cyclic control might have to be moved to the retreating side in order to fly straight at different airspeeds.

Thus in straight flight at constant speed, the cyclic stick must be held slightly towards the retreating side to counteract the inflow and coning induced rolls as well as forwards to counter the advancing/retreating induced pitch-up. In some machines the phasing of the controls is arranged so that forward cyclic automatically creates a degree of lateral cyclic. However, in the hover this results in the machine not responding precisely in the direction the stick is pushed.

Like the collective control, there is no one correct setting for the cyclic control. The cyclic trim control is used to shift the neutral position of the stick, relieving the pilot of the need to produce continuous control forces.

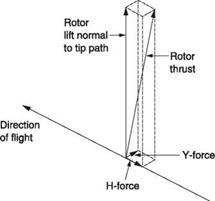
The retreating blade has the airspeed subtracted from the rotational speed and so has to operate with an increased angle of attack. The profile drag will be reduced but the induced drag will increase. Conversely the advancing blade will suffer significantly more profile drag because of the high relative airspeed, but the induced drag will fall because the angle of attack has been reduced. The overall effect of profile drag and induced drag does not balance between the advancing and retreating sides and the resultant is a rearward acting force called the H-force. Figure 3.26 shows that the H-force is the reason why the rotor thrust is not precisely at right angles to the tip path plane. A typical figure is 1°.

Because of inflow and coning, the blades crossing the nose produce more lift than the blades crossing the tail and so the induced drag is not the same. The resultant is the Y-force which acts at right angles to the direction of flight. The H-force is small and the Y-force is very small with the result that the effect on the magnitude of the thrust is insignificant.

Stall occurs when air passing over the cambered upper surface of a blade can no longer accelerate rapidly enough to follow the surface. Airflow breaks away and lift is lost

Fig. 3.26 H-force and Y-force. Conditions experienced by the blades in forward flight are asymmetrical and this reflects as cyclic differences in blade drag that produce a force in the plane of the rotor. The rotor thrust is not precisely at right angles to the tip path plane because of this force. H – and Y-forces are the components of this force in the fore-and-aft and transverse directions. The effect is very small and not really noticeable to the pilot.

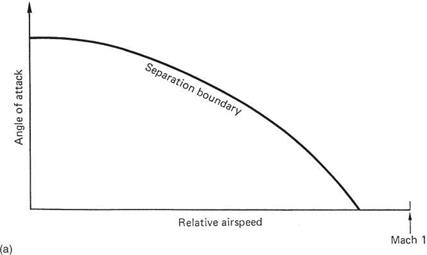
accompanied by an increase in drag. As acceleration is the limiting factor, at low relative velocities air can negotiate the blade at a larger angle of attack than at high velocity. Figure 3.27(a) shows the stall limit diagram for a typical section. As the speed of sound is approached, the allowable angle of attack becomes very small. Note that the speed of sound falls with falling temperature and in very low temperature conditions helicopters with high tip speed will suffer a performance loss.

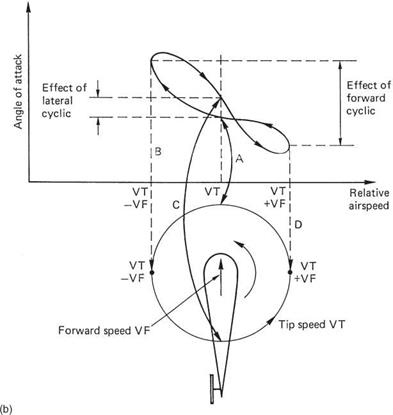
In fast translational flight, the tips of the rotor blades will be encountering relative airflow that alternately adds to and subtracts from the rotational speed. The pitch angle will change sinusoidally owing to the use of cyclic feathering but the angle of attack follows a more complex function owing to the effects of coning and inflow. Figure 3.27(b) shows the angle of attack of a part of the blade near the tip plotted against the relative airflow velocity. It will be seen that the plot is an elongated figure of eight. At positions A and C the blade movement is transverse, whereas at B and D the forward speed is subtracted from or added to the rotational velocity.

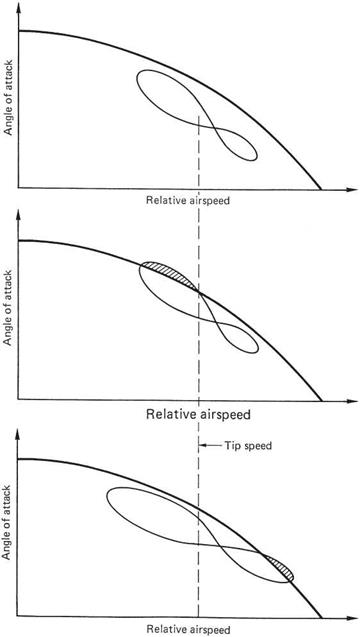
When the plot is superimposed on the stall limits of the airfoil section, it becomes possible to predict where blade stall will occur. This has been done in Figure 3.28. Figure 3.28(a) shows the conditions near the maximum airspeed. (b) shows that with a heavily loaded machine, stall can occur on the retreating blade where it has very low relative speed. The retreating blade needs to be feathered to a large angle of attack to resist lift asymmetry and inflow roll. The peak angle of attack will be reached at about 285° and the length of stalled blade will be greatest here. The loss of lift around 285° is converted by rotor phase lag to a pitch-up and roll. An attempt to correct the roll with cyclic will accentuate the stall and loss of control will result. Figure 3.28(c) shows that with a lightly loaded machine in straight and level flight or in a dive, advancing blade compressibility stall will occur first at high forward speed.

Partial blade stall can also be provoked at moderate speeds by tightly banked turns and if this is detected, the severity of the manoeuvre should be reduced immediately. Blade stall of either type causes serious vibration and control difficulty before the loss of lift becomes significant. Serious alternating stresses are set up and can cause blade delamination.

Fig. 3 .27 (a) As speed rises, air finds it increasingly difficult to follow the camber of an airfoil and the result is that the angle of attack must be limited as a function of speed to prevent stall. (b) The angle of attack of a blade may vary in the way shown here. The sinusoidal component due to cyclic pitch is modified due to variations in inflow over the disc.

(a)

(b)

(c)

Fig. 3.28 (a) No separation. (b) Retreating blade stall due to high rotor thrust. (c) Advancing blade compressibility at high airspeed.

The never exceed speed for the machine, Vne, will be set at a value which avoids advancing blade compressibility stall.

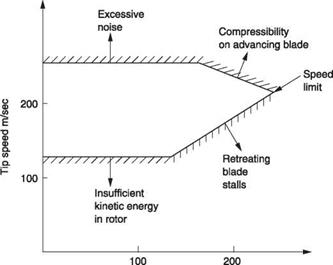
The pure helicopter is forever trapped in a forward flight region where it can retain control and contain blade forces. Figure 3.29 shows the constraints. The airspeed is added to the tip speed on the advancing blade, and this must be kept below about 0.92 of the speed of sound to avoid excessive noise and blade forces. On the other hand the airspeed is subtracted from the tip speed on the retreating blade and the advance ratio has to be kept below about 0.5 to avoid a large reverse flow area and retreating blade stall. As a result the pure helicopter with ideal tip speed is unable to exceed about 200 knots at the extreme right of the envelope of Figure 3.29.

If outright speed is not a priority, the possible range of tip speeds is greater. The upper limit is set by noise and the lower limit by the requirement to store enough kinetic energy to handle an engine failure. If a rotor has to provide thrust as well as lift it will be tilted well forward at high speed and the hull will be creating a lot of drag because of its nose down attitude. Higher speeds can be reached if an auxiliary form of forward thrust is available because the rotor thrust can then be vertical and minimized and the hull attitude will be better.

Westland modified the turbine exhausts to produce thrust on the speed record­breaking Lynx, and the Lockheed Cheyenne had a second tail rotor facing rearwards

Forward speed KT Fig. 3.29 Pure helicopter speed is forever limited by the coincidence of advancing blade compressibility and retreating blade stall at the right of the diagram. Only compound helicopters can break this limit using auxiliary thrust and/or wings to offload the rotor. At lower speeds tip speed is constrained by noise and stored energy limits.

to provide thrust for forward flight as well as a fixed wing to unload the rotor at high airspeeds. These ideas will be considered in Chapter 7.

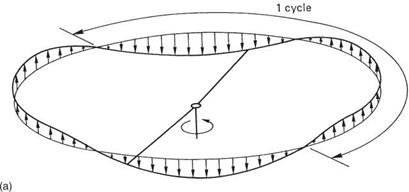
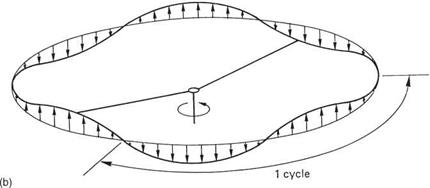
So far the disc has been discussed as an entity since the disc attitude determines the path of the machine. Now the motion of the blades within the disc will be explored.

In trimmed translational flight the application of cyclic feathering opposes the lift asymmetry. Cyclic feathering changes the blade pitch angle sinusoidally. If the lift asymmetry were also sinusoidal, the two effects would be in constant balance. Unfor­tunately this is not the case. Sinusoidal cyclic feathering is not strictly what is needed, but for practical reasons it is the most widely used solution. Cyclic feathering can only make the average lift moment the same on both sides of the disc. It cannot keep the lift of an individual blade constant at all angles of rotation.

Figure 3.30 shows what happens to a blade element as it rotates in forward flight with cyclic pitch applied. The diagram assumes uniform inflow across the disc and neglects coning for simplicity. Figure 3.30(a) shows the relative airspeed experienced by a blade element. The rotational speed produces a constant component, but the forward speed appears as a sinusoidal component to the revolving blade, adding speed to the advancing blade and subtracting it from the retreating blade. The lift generated by a blade is proportional to the square of the airspeed and this parameter is shown in Figure 3.30(b). Note that the squaring process makes the function at 90° very much greater than at 270°.

The coefficient of lift of the blade element is nearly proportional to the angle of attack. The collective pitch setting results in a constant component of the angle of attack and the cyclic pitch control causes this to become a shifted or offset sinusoid as shown in Figure 3.30(c). Figure 3.30(d) shows the lift function which is the angle of attack multiplied by the square of the airspeed. In other words waveform (d) is the product of (b) and (c). The amplitude of the cyclic control in (c) has been chosen to make the lift at 90° the same as the lift at 270°. Note that although the lift on the two sides of the rotor has been made the same by the application of cyclic feathering, the lift is not constant.

Unfortunately a sinusoidal function cannot cancel a sine-squared function. There is a lift trough at about 270° where the square of the relative airspeed has become very low and increasing the angle of attack fails completely to compensate. Lift symmetry is only obtained because the same cyclic input also strongly reduces the angle of attack at 90°. As a result there will be lift troughs at 90° and 270°.

The lift function contains a Fourier series of harmonics, or frequencies at integer multiples of the fundamental, which is the rotor speed. As the lift troughs on the two sides of the rotor are not the same shape, significant levels of odd harmonics will exist, especially the third and fifth harmonics. The lift function excites the blades in the flapping direction and they will respond according to the dynamic characteristics of the blade and its damping. The result is that the blades do not describe a perfect coning motion in forward flight, but as shown in Figure 3.31, they weave in and out of the cone due to the harmonics. Figure 3.31(a) shows second harmonic flapping, completing two cycles per revolution, whereas Figure 3.31(b) shows third harmonic flapping. The flapping action directly modulates the axial thrust delivered to the mast causing a hull motion variously described as ‘hopping’ or ‘plunging’.

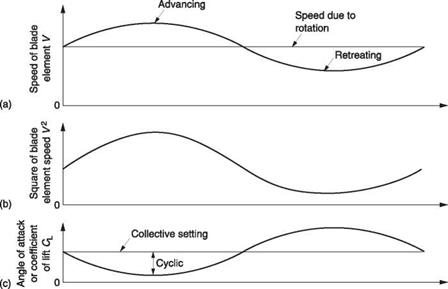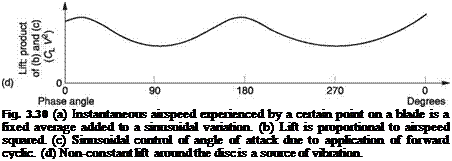Whilst vibration in the hover can be minimized by attention to dynamic balance and tracking, vibration in translational flight is inevitable because of the varying conditions caused by the alternate advancing and retreating of each blade. This causes harmonic flapping and dragging of the blades, resulting in forcing functions at the hub which may be axial, i. e. along the mast, lateral, i. e. tending to cause rocking, or torsional, i. e. tending to twist the mast.

On the retreating blade, the lift on the blade is concentrated near the tip with down­load near the root. This is because of the reverse flow area shown in Figure 3.22. As the same blade moves over the tail boom and into the advancing position, the lift dis­tribution changes so that the lift is now generated more inboard. If the blade is twisted, the angle of attack at the tip may be negative at high forward speeds resulting in a download. The situation is now exactly the reverse of the retreating case. Clearly the blade is being excited by time varying forces and as it is not rigid it will flex.

Fig. 3.31 Lift on a given blade is not constant, but a function of azimuth angle. This results in harmonic blade flapping. (a) shows second harmonic flapping. (b) shows third harmonic flapping.

Centrifugal stiffening keeps the blades taut giving them certain of the characteristics of the string of a musical instrument, except that the tension is not constant but is a function of radius. The response to excitation by a Fourier series is shown in Figure 3.32. A variety of harmonic structures will occur. At low frequencies the blade motion can be considered a form of flapping. At some higher frequency it will have to be considered a vibration. Note that blades carried on flapping bearings (a) will have a different harmonic response to that of hingeless blades. Teetering rotors and hingeless rotors have a different harmonic structure (b) from articulated rotors because the blades are fixed together in the centre of the rotor.

When a blade flexes, the CM of the blade elements must be closer to the rotor axis than when the blade is straight. Thus the blade mass is being hauled in and out against the rotational forces, modulating the blade tension. As the root tension is typically measured in tons, it should be clear that these lateral forces are considerable.

In the presence of harmonic flapping, conservation of blade momentum suggests that there will also be harmonic dragging. The azimuthal variation in lift caused by the application of the cyclic control will result in variations in induced drag that excite the blade in the dragging plane. This will be compounded by the azimuthal variation in profile drag. The blade will respond to these dragging excitations as a function of its dynamics and damping. When the blade drags, the effective moment-arm at which the blade outward pull is applied to the hub changes. Thus even if the blade pull were

(a)

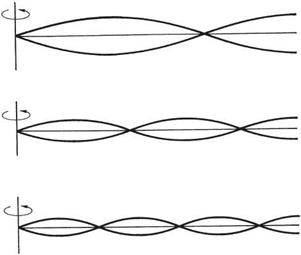
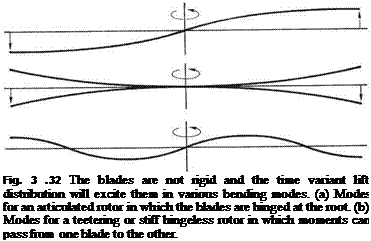
(b)

constant, the moment applied to the mast would be modulated. However, the blade pull is not constant because of blade flexing.

The application of cyclic pitch and the variations in airspeed seen by a blade segment will result in chord-wise movement of the centre of pressure which will excite the blade in torsion, placing alternating stresses on the pitch control mechanism.

A further complexity is that the finite number of blades in a real rotor cannot create a uniform downwash. The downwash velocity changes at the blade passing frequency. Figure 3.33 shows that in forward flight a given blade element traces out a path known as a cycloid. This path will take the blade element across its own path and those of a number of other blades depending on the forward speed and the number of blades. As the blade element crosses a previous path, the higher downwash velocity will reduce the angle of attack, whereas between the previous paths the angle of attack will increase. The result is that the lift of a particular blade element is modulated by the wakes of previous blades. Over most of the rotation the effect is generally not serious because

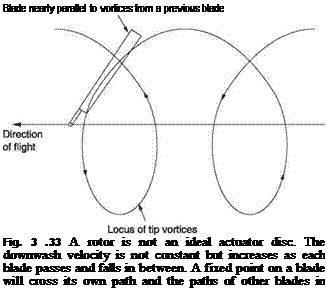the point on the blade at which the lift dips is constantly changing in radius. However, it can be seen from Figure 3.33 that at about 60° of azimuth the blade is nearly parallel to the cycloid, meaning that a significant length of the blade is experiencing the effect at the same time.

The non-uniformity of the downwash will also directly excite the hull and is com­monly observed as flexing of the canopy at the blade passing frequency. In the absence of vibration structurally transmitted from the rotor, this mechanism will still vibrate the hull.

In addition to the vibration sources noted above, in some flight regimes the rotor may ingest its own tip vortices. These are mostly carried away by downwash in powered flight or upwash in autorotation, but in some conditions, such as the end of a landing approach or a roll manoeuvre, the vortex from one blade may hit the next blade head – on. Figure 3.34(a) shows that the effect of a vortex approaching a blade is a local modulation of the RAF direction causing a dip in the angle of attack. Figure 3.34(c) shows that as the vortex leaves the blade the angle of attack is increased. The time taken for the blade to transit the vortex is only a few milliseconds and so the resulting pressure dipulse shown at (c) produces audio frequencies. This is the origin of blade slap.

In order to simplify study and to allow comparison between rotors turning at different speeds, the frequencies of vibration are always divided by the rotor frequency. Thus the units of vibration are not cycles per second but cycles per revolution. An imbalanced rotor will cause a lateral vibration at the rotor frequency having a vibration frequency of one cycle per rev. This is usually abbreviated to ‘one-per’.

In establishing the effect on the hull of vibrations created in the rotor, it is vital to appreciate that there are two completely different mechanisms at work. Vibrations in the direction of the mast axis and torsional vibrations about the mast axis are directly transmitted and will be felt in the hull at the same frequency. However, the rotor is turning with a frequency of its own and so vibrations in the plane of the rotor are taking place in a rotating frame of reference. When these vibrations reach the hull, which is in a stationary frame of reference, the same frequency will not be felt. Instead,

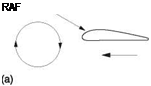
Blade approaching vortex – angle of attack falls

in the case of lateral (in-plane) directions the vibration frequencies beat or heterodyne with the rotor frequency to produce sum and difference frequencies.

The concept of sidebands was discussed in section 2.11, but the result can be demon­strated graphically. It is possible conceptually to replace the blade generating in-plane vibrations due to modulation of its root pull with a device generating the same vibration. This consists of a pair of contra-rotating eccentrics called a Lanchester exciter shown in Figure 3.35(a) which produces linear sinusoidal vibration. Figure 3.35(b) shows that if the rotor blades vibrate radially at the second harmonic (two-per) this can be simulated by an exciter which makes two revolutions with respect to the blade in one rotor revolu­tion. The result is that one of the eccentrics makes three revolutions with respect to the hull whilst the other makes only one. Thus a two-per in-plane blade vibration results in three-per and one-per at the hub in stationary co-ordinates. Third harmonic vibration produces four-per and two-per vibration in stationary co-ordinates and so on.

The discussion so far has considered the action of individual blades. However, in practice the hub will vectorially sum all of the forces and moments acting on it. Vectorial summation must consider the phase of the contributions from each blade. Clearly the phase difference between the blades is given by 360° divided by the number of blades. The overall result must then also depend on the number of blades in the rotor. If the blades are identical, and experience the same forces as they turn, they will develop the same vibration, except that the phase will be different for each blade. If, however, one blade has different characteristics to the others, a one-per function may result.

It is interesting to see how the number of blades affects the spectrum of vibration and how this effect is different for in-plane vibrations. Figure 3.36(a) depicts a two-bladed rotor and shows a graph of the fundamental flapping for each blade (one-per) and the second harmonic (two-per). Note that the two blades are 180° apart and so the one-per waveforms are in anti-phase and cancel. As one-per flapping is the result of tilting the disc this is no surprise and remains true for any number of blades. However, note that the second harmonic flapping of the two blades is in-phase and will therefore add.

(a) Fig. 3 .35 (a) A pair of contra-rotating eccentrics produces linear vibration. (b) If the mechanism of (a) is rotated, one of the eccentrics will turn faster and the other slower. Thus frequencies transmitted to the hull will be the vibration frequency plus or minus the rotor frequency.

It will be clear that a two-bladed rotor is at a disadvantage because both blades will be in the lift trough simultaneously at 90° and 270°, and in a lift peak simultaneously at 0° and 180°. The result at high speed is a vertical vibration known as 2Phop. Figure3.36(b) shows the situation for the third flapping harmonic. As the third harmonic flapping has one and a half cycles in the time between blade passings, it will be clear that the 3P components will be out of phase between the two blades. Following similar logic it should be clear that in a two-bladed rotor, only even vertical harmonics exist; the odd ones cancel.

Figure 3.37 shows the case for a three-bladed rotor. At (a) it will be seen that the second flapping harmonic waveform of each blade is at 120° to that of the next. The sum of three sine waves at 120° is constant and so there can be no 2P hop in a three-bladed

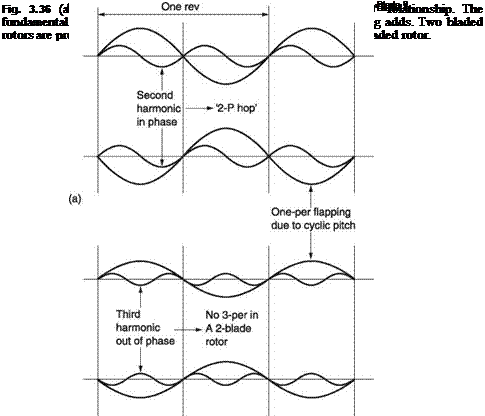rotor, or indeed for a rotor with a higher number of blades. In Figure 3.37(b) is shown the effect for the third flapping harmonic. Here the third harmonic waveform is in the same phase for each blade and so there will be summation.

Now that the general principle is clear, the result for any number of blades and any harmonic can readily be established. This is summarized in Figure 3.38(a) where it will be seen that the lowest hopping frequency is numerically equal to the number of blades and that these frequencies may be multiplied by integers to find the higher hopping modes.

When in-plane forces are considered, the results are quite different. Figure 3.38(b) shows the result of various harmonics with different numbers of blades. These forces will be heterodyned by rotor speed so that the result on the hull of a rotor frequency nP will be vibration at (n — 1 )P and (n + 1 )P whereas the frequency P is absent. Following the principles of vector summation explained above, certain harmonics cancel at the hub. Note that as with hop forces, the lowest frequencies at which rocking forces can exist are numerically the same as the number of blades, with the harmonics obtained by integer multiplication. The difference between Figure 3.38(a) and Figure 3.38(b) is that

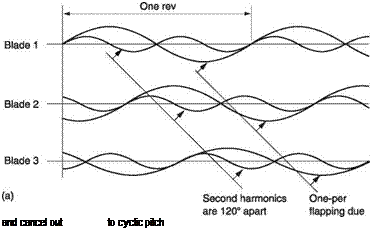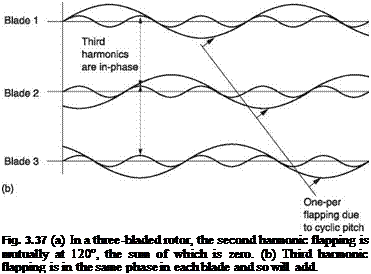different frequencies at the blades are responsible for the same frequencies at the hull. For example, a five-bladed rotor can suffer 5P hopping and rocking, but the hopping is due to blade flapping at 5P whereas the rocking is due to blade flapping at 4P.

This section has concentrated on the main rotor, but clearly a tail rotor will show many of the same effects as it too is passing edge-on through the air. However, the tail rotor is at a further disadvantage because it is working in airflow that has been disturbed by the main rotor and the hull. This will be considered further in Chapter 5.

Vibration and helicopters are inseparable. However well balanced the rotor may be, the lift asymmetry in forward flight will cause vibration. Vibration is unwelcome because

Number of blades 2 3 4 5 6 7 8 2P X 3P X 4P X X 5P X 6P X X X 7P X 8P X X X (a) Hopping or vertical harmonics

Number of blades 2 3 4 5 6 7 8 2P 3P 3P 2P 4P 4P 4P 3P 5P 5P 4P 6P 6P 4P 6P 6P 5P 7P 7P CL Q_ CD 00 6P 8P 6P 8P 8P 9P 7P (b) In-plane or rocking harmonics

Fig. 3 .38 (a) Axial or hopping modes as a function of the number of blades. (b) In-plane modes have different characteristics to axial modes because frequencies are heterodyned by the rotor frequency.

it has a number of negative effects. Section 3.26 showed some of the many causes of vibration and it should be clear that many of these may result in severe alternating stresses in the rotor head, the blade roots, the pitch control mechanism and the trans­mission. This has a large impact on the service life of such parts where a failure cannot be tolerated. Many parts need to have more generous cross-sections, increasing mass and reducing payload. Periodic checking for cracks adds to maintenance costs.

A key problem due to vibration is that it impairs the pilot’s vision. The human visual system (HVS) obtains its acuity by averaging visual information over a considerable length of time. In the presence of vibration, the image will be unstable on the retina and will thus appear blurred. There have been cases where damage to rotating components has caused vibration severe enough that the pilot was unable to read the instruments at all. Vibration contributes to pilot stress and workload. One of the earliest approaches therefore was to reduce vibration at the pilot’s seat.

Given the low load factor of a helicopter, the hull is not highly stressed and could be very lightly built were it not for fatigue inducing vibration. Increasingly helicopters incorporate electronic systems and sensors used either to control or navigate the machine or as part of its mission equipment. Electronic equipment does not take kindly to vibration, or if specially adapted, must be more expensive.

Vibrating masses are a common origin of sound, so it follows that a vibrating heli­copter will be noisy both inside and out. External noise causes disturbance in civil operations and may compromise military missions. A significant part of the design pro­cess of the modern helicopter is taken up in minimizing noise and vibration. There are a number of approaches that will be combined in various ways. Study of the aerodynamic origins of vibration may allow a reduction at the source. Once the forcing frequencies are known, the design of the structure should ensure that resonant responses to those frequencies are minimized. This is known as detuning. Vibration may be isolated or decoupled in some way, damped using lossy materials to convert flexing into heat, or opposed or absorbed through various cancelling techniques, both passive and active.

The reduction of the vibration at source has to be the technically superior solution. The disadvantage of decoupling the vibration from the passengers is that although their comfort is improved, the vibration experienced by the parts that are not decoupled may actually increase. It is easy to see why. For a given exciting force, the amplitude of a vibration is inversely proportional to the mass being vibrated. In a conventional helicopter the dominant masses are those of the transmission, hull and payload. If the hull and payload are decoupled, the mass seen by the vibration source is now only that of the transmission and the amplitude of the vibration there must be greater and not necessarily beneficial.

An obvious way of reducing vibration at source is to use non-sinusoidal cyclic pitch control that allows the lift moment to be more nearly constant as the blade turns. The means to do this are non-trivial and are described in section 3.28. Another way of reducing vibration is to use more blades. This has several advantages. First, the load on each blade is reduced and with it the magnitude of the forcing function of each blade. Second, the more blades, the higher the frequency of the vibration will be and the lower will be the amplitude for a given mass. Figure 3.37 shows that a three – bladed rotor eliminates the 2P hop of the two-bladed rotor, whereas a four-bladed rotor reintroduces some 2P lateral vibration. It will be seen from Figure 3.38(b) that an even number of blades gives lower rocking frequencies, making an odd number preferable. Consequently the change from four to five blades gives a significant improvement. Large transport helicopters inevitably have a large and generally odd number of blades – seven or nine – simply to contain the large vibrations that must result from generating high rotor thrust. Using many blades will be expensive and result in a large rotor head having high drag.

It is common to design the blades so that their natural frequencies of vibration are not in the spectrum of the excitation. If any of the excitation frequencies coincide with the resonant frequencies there could be a significant response at that frequency. Any coincidence can be seen from an interference diagram as shown in Figure 3.39. This interference diagram is for the Westland Lynx and shows the operating speed (318 RPM) as a vertical line. The excitation frequency may be at any integer multiple of the rotor frequency. Figure 3.39 shows that, as rotor speed increases, the excitation harmonics (thin lines starting at the origin) fan out. The resonant frequencies of the blades also change with rotor frequency because of the effect of centrifugal stiffening. Figure 3.39 shows how flapping, mf, and lagging, ml, resonant frequencies may change with rotor speed.

The only coincidence between excitation and response is the close correspondence between the fundamental flapping resonant frequency and the rotor fundamental fre­quency. This is the characteristic that results in rotor precession. Note that as the Lynx

Fig. 3.39 The excitation spectrum in a rotor fans out at RRPM increases. The natural frequencies of flapping and dragging of the blade will also change with RRPM due to centrifugal stiffening. If these two effects are superimposed, it is possible to see where the excitation frequencies coincide with response frequencies. This is known as an interference diagram. (AugustaWestland)

has a hingeless rotor, the flapping resonance is above the rotor frequency and so the rotor phase lag will be less than 90°.

In all other cases, coincidence is avoided so that at normal RRPM no resonances are excited. This result was not an accident. During the design process the blade was designed with a tapering spar resulting in the stiffness and the mass per unit length being non-uniform so that the flapping resonant frequencies are not integer multiples of the fundamental. Where constructional techniques such as extrusion do not allow the blade or spar to taper, the blades can also be detuned by placing weights at critical points along the span so that the effective mass per unit length is no longer uniform. Note that the technique of detuning only works at one rotor speed, at other speeds the excitation frequency is different and the response will also differ. Detuning will also be employed in the hull so that hull resonance does not magnify rotor-induced vibrations.

Although vibration may occur at a number of frequencies, often one of these will dominate and cause a problem. Vibration absorbers are devices intended to reduce vibration at a single specific frequency. The term is actually a misnomer because what they actually do is to create an opposing or near-anti-phase vibration. These devices work using mechanical resonance.

As was seen in section 2.9, a mass supported on a spring displays resonance. If the damping is very low, the phase response just above the resonant frequency becomes nearly 180°. If the resonant frequency is set just below the frequency of vibration, the mass will automatically resonate in inverse phase and oppose the vibration. In helicopters the battery may be used as a suitable mass and this is supported on carefully calibrated springs. A mass absorber of this kind can only reduce vibration in the vicinity of the device itself. Flexibility of the hull will allow vibration elsewhere; however, such devices can oppose the hull vibration due to non-uniform downwash. Mass absorbers only work at a fixed frequency and require the rotor to turn at a precisely controlled RPM. The alternative is to use a system in which the spring stiffness can be modified by a servo so that the absorber can be tuned to the actual RRPM in use. Such a system is fitted in the Chinook. In some early helicopters vibrations fed into the control rods were opposed in this way. Figure 3.40(a) shows a resonator consisting of a bob weight on a leaf spring attached to a control bell crank.

A pendulum is a kind of resonator. The type used in a clock uses the earth’s gravita­tional field to provide the restoring force. In helicopters, pendular vibration absorbers fitted on rotors use the acceleration caused by rotation. Figure 3.40(b) shows that pen­dular absorbers used to handle flapping vibration consist of weights that can swing on the end of cranked shafts pivoted in the blade roots. When the rotor is turning, the weights fly out horizontally and attempt to stay in the same plane. Vertical movement of the blade excites the pendulum which is tuned to resonate in anti-phase. These devices can be seen on the Kamov Ka-32 and on the Bo-105 and are known colloquially as bull’s balls.

As these devices employ resonance, a single unit can only oppose vibration at a single frequency. However, it is possible to fit more than one pendulum to the same mounting. The Hughes 500 has a four-bladed rotor and so according to Figure 3.38(b) will be prone to 4P rocking forces due to flapping at 3P and 5P. The two pendula are tuned to the third and fifth harmonics of blade flapping.

Torsional vibration of the rotor shaft may be due to blade excitation in the dragging plane. This is an application for the bifilar pendulum. A pendulum can be made to swing in one axis only by attaching it with two strings, hence the name. Restoration forces are much smaller for in-plane motion, suggesting that a pendulum would need a very short arm in order to resonate at a harmonic of rotor frequency. Thus in practice the arms are replaced by a pair of pins which operate in oversized holes as in Figure 3.40(c). As the weight moves to one side, the geometry of the pins moves the weight inwards. As the weight tends to fly out as the rotor turns, there will be a restoring force if the weight is displaced. This is all that is necessary to create a resonant system.

The restoring force that determines the resonant frequency in pendulum and bifilar absorbers comes from the acceleration due to rotation. This is a function of RRPM, as is the frequency to be absorbed. Consequently these devices are self-tuning.

Another popular and obvious way of isolating vibration is to use flexible mountings between the transmission and the hull. It is a fundamental concept of such mounts that there will be a resonance whose frequency is determined by the sprung mass and the stiffness of the mounts. The degree of isolation is proportional to the difference between that resonant frequency and the frequency to be filtered out. Consequently the lowest possible resonant frequency is required. This frequency may be lowered by

Fig. 3.40 (a) A bob weight on a leaf spring attached to a bell crank will oppose vibrations in a control run. (b) The pendular absorber is designed to oppose vibrations in the axial direction. (c) A bifilar pendulum absorber achieves the effect of very short arms by using rollers as shown here.

softening the mounts, or by increasing the supported mass. Soft mounts may cause other problems, such as handling difficulties because the hull would tend not to follow the rotor in a manoeuvre. As a result, the best solution is to increase the mass to be isolated as much as possible.

This is the principle of the machinery raft, which is a rigid structure carrying the engines, transmission, control actuators, oil coolers, generators, etc. as a single unit. This raft is then mounted to the hull by widely spaced resilient supports. The large mass of the raft opposes the forcing function of the rotor and makes the resonant frequency as low as possible, as well as reducing the amplitude of vibration seen by the components on the raft.

The problem with resilient supports is that for good isolation they have to be soft, and this will always result in a static deflection. Some techniques have been developed for helicopters to circumvent the problem. Figure 3.41(a) shows a system developed by Kaman known as DAVI, or dynamic anti-resonant vibration isolator. This works using a mechanical impedance convertor to raise the moving mass artificially. Between the transmission and the hull is a lever carrying a bob weight. The mechanical advantage of

Transmission mounted here

Hull suspended here (b) Fig. 3.41 (a) In a dynamic anti-vibration isolator, a lever is used to amplify the motion of a weight thus giving it enormously increased effective mass. (b) The nodal beam system. A suitably tuned flexing beam will have nodes where the hull is attached.

the lever causes any relative motion to be amplified. The lever changes the mechanical impedance of the bob weight by a factor equal to the square of the mechanical advan­tage. Thus a 1 kg weight on a 10:1 lever would appear to weigh 100 kg. Mounting the transmission on, for example, four such mounts would raise the effective weight by 400 kg. Given the increase in apparent weight of the transmission, the supporting spring can be made much stiffer than would be possible with a conventional resilient mount, without increasing the resonant frequency.

Figure 3.41(b) shows the nodal beam system developed by Bell. At one time most Bell helicopters had two blades and suffered 2P hop. The nodal beam was developed to isolate the hop. Between the hull and the transmission is a flexible beam made from a sandwich of elastomer and steel. The transmission mounts are closer together on the beam than the hull mounts. As relative movement takes place between the hull and the transmission, the beam must bend. The proximity of the hull and transmission mounts makes a virtual lever system resulting in larger amplitude of movement at the centre of the beam. The effective mass of the beam is amplified by the mechanical advantage of the virtual levers, making the system mathematically equivalent to a pair of DAVI isolators in parallel. The geometry of the system is tailored so that at the bending resonant frequency of the beam the hull attachment points are at nodes and so do not move.

In active vibration cancelling systems, Figure 3.42, a number of high speed actuators, typically hydraulically operated, are used to attach the hull to the transmission. The actuators are controlled by signals from processors and accelerometers in the hull. The signal processors are needed to adapt the waveforms fed to the actuators to changing conditions such as all up weight and airspeed. An increase in all up weight would

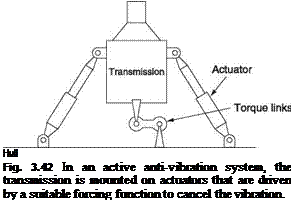require increased static pressure in the actuators to prevent them extending. In practice a feedback mechanism measures the average extension of the actuator and centralizes each one with a relatively long time constant.

No practical hull can be rigid, and so there will be various modes of vibration excited in it. One of the sources of vibration will be due to the non-uniform downwash imping­ing on the hull surface. Conventional isolators between hull and transmission can do nothing about this because they only oppose structure-borne vibration. However, an active system can use the transmission as a reaction mass to create forces opposing vibration from any source. Unfortunately the amplitude of vibration in the transmis­sion will be increased. Better results may be obtained by applying active control to a raft carrying the engines, etc. as described above.

It was seen in Figure 3.30 that the use of sinusoidal feathering in a cyclic pitch control is incorrect. The airspeed seen by a blade element changes sinusoidally in forward flight, but the lift is proportional to the square of the airspeed. This non-linear function gen­erates flapping harmonics that cannot be cancelled by sinusoidal feathering. It follows immediately that if there are to be no flapping harmonics, the feathering function must contain harmonics.

A harmonic cyclic pitch waveform is approximately a square root function of a raised sine wave although some modification will be necessary because of inflow effects. When multiplied by the sine-squared function due to the speed, the product, namely the lift, is constant. The pitch function above will need further refinement to account for upwash at the leading edge of the disc. Figure 3.43 shows how an actuator between the swashplate and the blade control arm could add the harmonic control.

In practice perfect constant lift can only be achieved at one radius, but it should be possible to find a pitch function that makes the average blade lift moment essentially constant. A more advanced system would have means to control the angle of attack of different parts of the blade independently. This may be possible using, for example, piezo-electric actuators. It is impossible to obtain constant lift over the whole blade because of the reverse flow area, and so some harmonic flapping will always remain.

Whilst theoretically obvious, harmonic blade control, also known as higher harmonic control, is rarely found. One of the difficulties is that the cyclic control becomes a

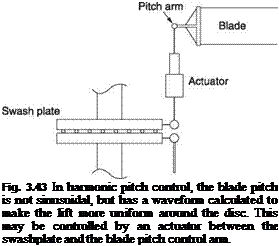function of airspeed, returning to a near sinusoidal function in the hover. This is probably beyond what might be achieved mechanically but some kind of electronic system would easily generate the required functions. High speed actuators are necessary to drive the blade feathering, and the blades must be torsionally stiff in order to respond to the rapid pitch variations. Another consideration is that as the number of blades increases the effects of lift troughs are averaged out more and there is less of a problem.

However, the elegant result of constant lift moment around the disc is one that is most desirable. The reduction in vibration makes the flight more comfortable for passengers and prolongs the life of the machine. A further consequence of constant lift is a reduction in power needed in forward flight. In a conventional rotor the increased power needed where the lift is greatest is not balanced by a reduction in power where the lift troughs are. Consequently constant lift needs the least power.

It would seem clear that the greatest cost benefit of harmonic blade control would be in the two-bladed helicopter where the 2P hop could be eliminated. The improvement in ride would be greatest but the number of actuators needed is least. In some light helicopters a two-bladed harmonically controlled rotor could replace a conventional three-bladed rotor and the overall cost might be the same. At some point designers will find ways of economically achieving the goal of constant lift. Some experiments have been done with systems which rock a conventional swashplate, but this cannot give the required result as each blade needs to be individually controlled.

The helicopter blade is a complex subject because of the number of interacting variables involved. These will be considered here. It might be thought that the aerodynamic characteristics of the blade would be determined only by shape. In general this is untrue. Figure 3.44 shows some of the issues. The long thin structure of a practical blade can never be rigid and flight loads will cause the blade to flex. However, it is not enough to know the stiffness of the blade to calculate the result. In forward flight the loads have a powerful alternating component and this generates harmonics. At the frequencies of the higher harmonics the motion may be mass controlled. A further complexity is that the flexing of the blade will affect the aerodynamics; a phenomenon

Fig. 3.44 The aeroelasticity effect loop in a rotor blade. The blades are not rigid and can flex. This will affect their local angle of attack, changing the lift distribution that in turn causes flexing.

Fig. 3.45 (a) If the blade has greater bending stiffness at the leading edge, it will wash out as lift increases. This is a stable condition as wash-out reduces the lift. (b) If the trailing edge is stiffer than the leading edge, lift causes wash-in that will further increase the lift. Such a blade would suffer serious flutter and probably disintegrate.

called aeroelasticity. As it is clear that the aerodynamics affect the flexing, then there is a loop. This loop may be stable or unstable. Part of the design process must be to ensure that aeroelastic effects always result in blade stability.

The shape of the blade is completely defined by the root cut-out, the tip shape, the degree of twist and taper and by the blade section used, which may change with radius. Assuming first a rigid blade, the blade shape will allow the time variant aerodynamic forces to be predicted in a given flight regime. The way the blade responds to this excitation is complicated. The torsional forces depend on the locus of the centre of pressure with respect to the mass centroid. The effect of flight loads on blade twisting is significant because twist will alter the local angle of attack as well as feeding loads back into the control system. The degree of twisting depends on the moment of inertia, the stiffness, the damping and the frequency.

The chord-wise distribution of stiffness needs to be known accurately. Figure 3.45(a) shows a blade in which the leading edge is stiffer than the trailing edge. The application of lift at the centre of pressure causes the blade to wash out; a stable condition. However, Figure 3.45(b) shows a blade in which the trailing edge is stiffer than the leading edge. Here lift causes the blade to wash in; leading to flutter. As a result blades are generally constructed in such a way that the mass centroid and the centre of bending stiffness is well forward on the chord. The result is a section where the structural mass is concentrated in a D-shaped structure at the leading edge, with the trailing part of the section being comprised of a low density structure.

Blade taper is not always employed because in practice the penalty of a constant chord blade is only a few per cent. Taper prevents constructional techniques such as extrusion that requires a constant section. Blade twist is advantageous in hover, but the ideal amount for hover will be detrimental in translational flight because the application of cyclic pitch may cause the finely pitched blade tips to go to a negative angle of attack. The exception to this restriction is in the tilt rotor aircraft that both hovers and cruises with axial inflow. This gives the designer more freedom to use blade twist and this is clearly visible in rotors of the Bell-Boeing Osprey.

4