Longitudinal motion of the helicopter

To analyze the longitudinal dynamic stability characteristics of the helicopter it is necessary to consider the equations governing its motion. In order to study these equations, simplifying assumptions are required to ease the computational task. The matrices describing the equations of motion often include several acceleration depend­ent derivatives such as M„-. Assuming all these are negligible and the centre of gravity is aligned with the main rotor drive shaft such that dx = dy = dz = 0, then:

control theory when applied to multi-input/multi-output (MIMO) systems states that the Characteristic Equation (CE) can be obtained from the following:

det(sI — A) = 0

where A is the result of pre-multiplying Ma by M. The CE when solved will show the nature of the controls fixed response of the helicopter to a disturbance. So:

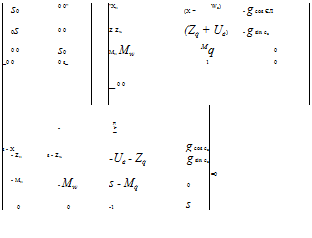
= 0

This determinant will be of the form, As4 + Bs3 + Cs2 + Ds + E = 0, where the coeffi­cients in the polynomial can be expressed in terms of aerodynamic derivatives, see Bramwell [4.1]. The quartic may be solved by numerical computer methods when the values of the coefficients are known. Consequently the characteristic equation can be evaluated and factorized. For helicopters, in most cases, the equation factorizes to:

(T s + 1)(T2 s + 1)(s2 + 2^mn s + m2) = 0

The three modes of motion implied by this equation are summarized below:

(1) Vertical velocity mode. The vertical velocity mode, described by (Tts + 1) = 0 is a stable, heavily damped subsidence in vertical velocity. The motion is decoupled from speed and pitch and has a time constant of the order of 1 to 2 seconds.

(2) Forward speed mode. The forward speed mode, described by (T2s + 1) = 0 is a stable, heavily damped subsidence in speed. The motion is coupled with pitch attitude and pitch rate. It has a short time constant of the order of 0.5 second.

(3) Pitching oscillation. The stability of the pitching oscillation is both speed and flight condition dependent. In the climb or at high speed the oscillation can be unstable, possibly degenerating to an exponential divergence at high speed. The oscillation couples with the forward speed mode and is mainly due to rotor flapping caused by speed changes.

These basic equations of motion govern the aircraft in all flight regimes but differing values of the derivatives account for differences in the behaviour and will, of course, give different characteristic equations to solve. It should be remembered that all modes will be excited following a disturbance or pilot input. The various dynamic modes described above can be separated into long-term modes and short-term modes. The long-term modes characterize the dynamic stability of the helicopter, whereas the short-term modes affect the pilot’s perception of the aircraft during manoeuvres, that is its control response.