Perturbation Equations of Unsteady Flight

With a good understanding of perturbed steady flight, we can branch out and derive the perturbation equations for some important unsteady maneuvers. We focus on those flight conditions that maintain significant angular velocities, like the pull-up maneuver of an aircraft and the circular engagement of an air-to-air missile. In both cases we start with Eqs. (7.38) and (7.39), the general perturbation equations of unsteady flight and use the expansions of aerodynamic derivatives, Eq. (7.53) and (7.54). The resulting equations, expressed in state-variable format, are quite useful for specialized dynamic investigations of unsteady flight.

7.5.1 Aircraft Executing Vertical Maneuvers

Pull-ups of aircraft or push-down attacks of cruise missiles are maneuvers with sustained pitch angular velocities. They occur in the vertical plane and are sym­metrical maneuvers in the sense that the yawing and rolling rates are near zero. We proceed with expressing the perturbation equations in components, starting with Eq. (7.38).

The state variables are the linear and angular velocity perturbations

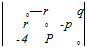[evg]5p = [u v w], [єшВІ]Вр = [p q r], [eQ, BI]Bp —

and for vehicles with planar symmetry, like aircraft or cruise missiles, the MOI tensor (same in reference and perturbed body coordinates) is

Now we specify the components of the reference maneuver. Because it is executed in the vertical plane, only the linear velocity components ur and wr and pitch rate q, are nonzero:

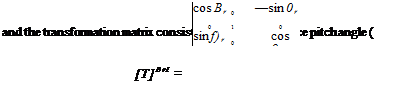[^r]5r = (Mr 0 uvl. o>’MBr = [0 q, 0], QBr/]Br

Substituting these components into Eq. (7.38), multiplying out the matrix products, and rearranging terms, yields the translational equations

й		—qrw — wrq		—COS0re	1 + — m	efa)Bf
І)		—urr + wrp	+ £	sin0rl/f + cos вгф
w		qru + urq		—sin 6r0

The same substitutions into Eq. (7.39) lead to the rotational equations InP + /13/ ~hiP + (h – І33У (ema)Bxp hq = qr 0 + (sma)Bp InP + /33/ (hi ~ h)p + Inr _ (ema)Bp

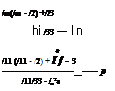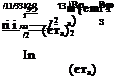which, however, require further modifications. The left-hand side consists of more than one state vector derivative in the first and third components. The excess must be removed to arrive at a true state-variable representation. The terms I^r and /ізp can be eliminated by the following manipulations: 1) multiply the third row by /із and subtract it from the first row multiplied by /33, and 2) multiply the first row by /13 and subtract it from the third row multiplied by Iu. Neglecting terms that are multiplied by the small factors /із//33 and In/In furnishes finally the desired format:

Equations (7.75) and (7.76) are the perturbation equations for vertical maneuvers. On the left-hand sides remain only the time derivatives of the state variables. The effect caused by the unsteady reference flight is arranged in the first terms on the right-hand sides of the equations.

The gravity term of Eq. (7.75) is a function of the reference pitch angle, which can vary between 0 and 90 deg. Its perturbation variables are the Euler angles. The last terms of the dynamic equations contain the aerodynamic force and moment derivatives. We turn now to their assessment.