Pitch Dynamic Equations

The uncoupled pitch dynamics consist of the pitching moment equation, second of Eq. (7.56), and the normal force equation, third of Eq. (7.55). This example is for tetragonal missiles. We therefore use Fig. 7.2 to write down the nonvanishing linear derivatives

I2q = Mww + Mqq + + MSq8q

Instead of w we prefer the expansion in terms of the angle of attack a and merge M& into Mq (quite common for missiles). Furthermore, to conform to conventions the derivatives are divided by the pitch moment of inertia /2 but retain their letter symbol M:

q — Маа + Mqq + Msq8q (7.58)

We model the normal force dynamics by the third component of Eq. (7.55). Neglecting the gravitational term and the centrifugal term mqur, we have (but see Problem 7.6)

mu> = Zww + Zqq + Z^w + Zsq8q (7.59)

Again, we replace w by a, neglect all damping derivatives, and furthermore follow missile conventions, replacing Z by —N (normal force) and the vertical accelera­tion u> by the normal acceleration —a. Redefining the normal force derivatives N by including the mass in the denominator, we formulate

a = Naa + N$q8q (7.60)

Equations (7.58) and (7.60) will be used for an acceleration autopilot design with inner rate-loop damping. Commonly, only pitch gyros and accelerometers are available as sensors, but not angle of attack. The a dependency must therefore be eliminated. You accomplish this feat by first taking the derivative of Eq. (7.60):

a = Nade + Nsq8q (7.61)

Then recalling that the normal acceleration a is proportional to the flight-path-angle rate у (f°r small a).

a = Vy (7.62)

and with the kinematic relationship у = q — a

a=Vy = V(q— a) (7.63)

Solving for a and substituting into Eq. (7.61)

Na

a = Naq – —a + NSq8q (7.64)

Now, premultiply Eq. (7.58) by Na and (7.60) by Ma, subtract them from each other, and then solve for q. You derived the important result without a dependency:

і, Ma (MaNgq^ /-7 сеч

q = Mqq + — a + I MSq———– 1 JSq (7.65)

Equations (7.64) and (7.65) are the state equations for a and q. The derivative of the pitch control Sq of Eq. (7.64) is acquired from a first-order actuator, as shown in Fig. 7.3. It provides the third state equation

Sq = Xu — kSq (7.66)

with и the commanded input and 1 /X the actuator time constant. Substituting this Sq into Eq. (7.64) yields

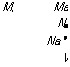Collecting the three equations (7.65-7.67) yields the desired result:

These state equations in pitch rate q, normal acceleration a, and pitch control Sq are quite useful for autopilot design. Particularly, we succeeded in replacing a by a, therefore replacing the difficult to implement angle-of-attack sensor by the readily available accelerometer from the INS.

Fig. 7.3 Actuator dynamics.

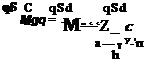The dimensional derivatives Na, NSq, Ma, Mq, Mgq are related to the nondi- mensional derivatives CNa, CNSq, Cm„, Cm?, Cmsq by

where d is the missile diameter and S the maximum cross section.

Sometimes autopilots are designed without consideration of actuator dynamics. For these simplified circumstances we set Sq = 0; thus, fromEq. (7.66) Xu = XSq. Neglecting N$q Ma/Na against the significantly larger Мц, we gained the reduced – order state equations

(7.69)

These pitch-plane equations, which depend on pitch rate q and normal acceleration a as state variables only and have the pitch control 8q as input, play an important role in the design of air-to-air missile autopilots. Because of their simplicity as plant descriptor, a self-adaptive autopilot can be constructed around them. I present the details in Sec. 10.2.2.4.

The discussion would be incomplete, however, without also reintroducing the angle of attack as one of the state variables. Substituting Eq. (7.63) into Eq. (7.61) eliminates the acceleration a completely, and we are left with

8q

which we use to replace the a equation in Eq. (7.69):

We will make use of this format when we design the rate autopilot in Sec. 10.2.2.1. There, we will derive the q(s)/8q(s) transfer function by eliminating a, thus by­passing the need for an a sensor.

Similarly, the lateral acceleration equations with the state variables’ yaw rate r and sideslip angle f}, and the control input 8r are (see Problem 7.1)

(7.71)

where LN designates the yawing moment derivative (to avoid confusion with the normal force derivative N).