Roll/yaw inertial coupling

Finally, we use the third of the attitude equations, Eq. (7.85),

qrp(I – h) , N

r =————————–

h h

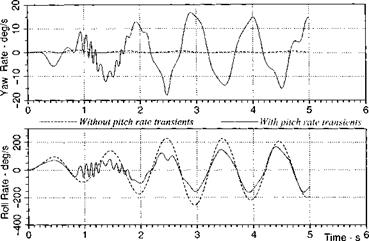
and study the inertial coupling of roll rate p into yaw rate r in the presence of a sustained pitch maneuver qr. A new reference trajectory is needed. With a pitch control of 1 deg, we generate a planar trajectory whose pitch rate qr peaks at — 150 deg/s and its angle of attack a at —30 deg. Now we excite the roll channel with a sinusoidal roll control input of 0.1-deg amplitude and 1-s period. The coupling of roll via pitch into yaw is shown in Fig. 7.8. In the presence of pitch – rate transients, the yaw rate is oscillatory with the period of the roll perturbations and peaks at 15 deg/s. If the pitch control is zeroed, the missile flies ballistic, and the coupling of roll into yaw disappears.

In summary, the perturbation equations of missiles during unsteady flight were derived from the general six-DoF equations of motion, and the aerodynamic forces and moments expanded in the Taylor series up to second-order terms. With these equations we interpreted the results of a six-DoF air-to-air missile simulation.

The aerodynamically induced rolling moment couples into the pitch channel during a yaw maneuver. The yaw channel is excited by rolling motions in the presence of a pitch maneuver. All three attitude channels are mutually linked by aerodynamic and inertial coupling.

These perturbation equations give insight into the dynamics of agile missiles. They shed light on the stability characteristic and should guide the control engineer in suppressing unwanted coupling effects.

Fig. 7.8 Yaw-rate response caused by roll oscillations in the presence and absence of reference pitch rate.

With these rather sophisticated dynamic escapades, I conclude Part 1. I hope you enjoyed the ride and did not fall asleep earlier from sheer exhaustion. We solved simple geometrical problems, wrestled with the kinematics of translation and rotation, and derived the equations of motion thanks to Newton and Euler. We followed our motto “from tensor modeling to matrix coding” faithfully and saw no reason to deviate from the hypothesis that all dynamic problems can be formulated by points and frames. If you solved the majority of the problems at the end of each chapter, you should have reached the pinnacle of dynamic bliss.

Now has come the time to put all theoretical knowledge to practical use. As the structure follows the blueprint, so do simulations proceed from modeling. In Part 2 you will be challenged to put your new-found skills to work and develop three-, five-, and six-DoF simulations.

References

‘Etkin, B., Dynamics of Atmospheric Flight, Wiley, New York, 1972.

2Hopkin, H. R., “A Scheme of Notation and Nomenclature for Aircraft Dynamics and Associated Aerodynamics,” Royal Aircraft Establishment, TR66200, Famborough, U. K., June 1966.

3Noll, W., “On the Continuity of the Solid and Fluid States,” Journal of Rational Mechan­ical Analysis, Vol. 4, No. 1, 1955, p. 17.

4Maple, C. G., and Synge, J. L., “Aerodynamic Symmetry of Projectiles,” Quarterly of Applied Mathematics,” Vol. 6, Jan. 1949, pp. 315-366.

5Zipfel, P. H., “Aerodynamic Symmetry of Aircraft and Guided Missiles,” Journal of Aircraft, Vol. 13, No. 7, 1976, pp. 470-475.

6Pamadi, B. N., Performance, Stability, Dynamics, and Control of Airplanes, AIAA Ed­ucation Series, AIAA, Reston, VA, 1998, Chap. 4.

Problems

7.1 Yaw stability equations. To support the design of a simple yaw damper for an aircraft, you are requested to derive the state equations of yaw rate r and sideslip angle /6. Start with the linear perturbation equations (7.55) and (7.56) and use linear aerodynamic derivatives. The desired form is

LN? I	r		Г LNsrl
Г0	A	+	YSr
V.		. V.

Sr

State clearly the assumptions that lead to this formulation.

7.2 Fill in the details. Apply your tensor manipulative skills and fill in the intermediate steps between Eqs. (7.16) and (7.17).

7.3 Missile linear perturbation equations over the flat Earth. Start with Eqs. (7.55) and (7.56) and derive the full linear dynamic equations of a missile with tetragonal symmetry. Which equations are coupled? Can you group them into two uncoupled sets? Compare your equations with the stability equations for aircraft in Pamadi’s book.6

7.4 Aircraft pitching moment derivatives. Expand the M derivative of an aircraft up to second order.

7.5 Six-DoF aerodynamic model. You are asked to develop the aerodynamic model for a six-DoF aircraft simulation. Mach number and angle of attack vary extensively so that you are directed to build your aerodynamic coefficients as ta­bles in M and a. The other variables fi, a, fi, p, q, r and the controls 8a, Se, 8r experience only small excursions and are therefore to be modeled by linear deriva­tives. The aircraft reference area is S, its mean chord c, its span b, and its speed V. Write down the aerodynamic force and moments in terms of the nondimensional stability and control derivatives.

7.6 Effect of Centrifugal Term. The state space formulation, Eq. (7.68), of rate and acceleration dynamics is very useful for controller design. We obtained this simple form by neglecting gravitational and centrifugal terms. Now, you are to derive the terms that we neglected, because of disregard of the centrifugal effect. Conduct the derivation that leads to Eq. (7.68), starting with Eq. (7.55) but without neglecting the centrifugal term. Compare the two formulations and discuss the effect of the centrifugal term on rate and acceleration dynamics.