. Tangential Velocity

Just as in hovering, the momentum, or energy, method is useful in understanding the physics of forward flight and for making rough calculations; but the blade element theory must be used to define flight limitations and to do more accurate calculations. In forward flight, the velocity acting on the blade element is a function of both the radial station and the blade azimuth position.

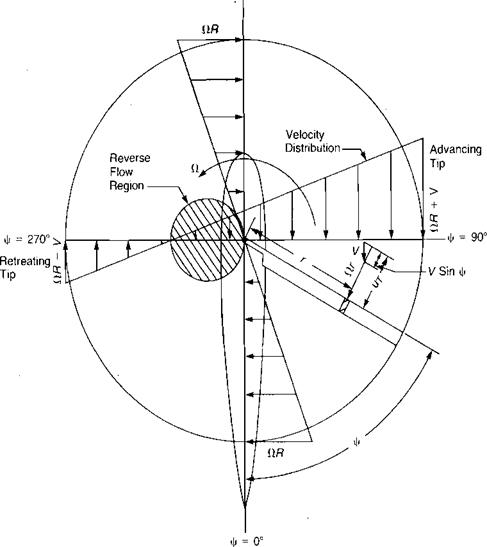
The azimuth angle, |/, is defined as shown in Figure 3.14 with |/ = 0 over the tail. The velocity acting on the blade element is the vector sum of the velocity due to rotation, fIr, and the forward speed of the helicopter, V. The study of swept – wing aerodynamics has shown that the component of velocity perpendicular to the leading edge is the only velocity that is important in establishing aerodynamic forces. The velocity perpendicular to the leading edge—or tangential to the chord of the element—UT, is:

Uf = Clr + Fsin|/

Over the tail and over the nose, the blade element sees the same velocity as it would in hover, but on the advancing blade it sees a higher velocity, and on the retreating blade a lower. As a matter of fact, on the retreating blade there are elements where the velocity perpendicular to the leading edge is actually negative—that is, air strikes the trailing edge rather than the leading edge of the blade. Figure 3.14 shows the vector addition of the velocities for the blades at the cardinal azimuth positions. If the equation for UT is set to zero, the radius station at which the velocity vanishes is:

sin |/

A plot of this relationship is a circle that is tangent to the rotor centerline. Inside this circle, UT is negative, and the zone is called the reverse flow region.

Using the definition of the tip speed ratio, Ji, the equation for the tangential velocity may now be written:

UT = flR — + p sin j/

V R /