Acceleration controller

Let us start with the heart of a missile autopilot. It consists of body rate and acceleration feedback with lead/lag shaping filters as depicted in Fig. 9.9. For five-DoF modeling we simply represent the rate feedback loop by a first-order transfer function with the time constant TR, which is representative of the full rate autopilot response. If the flight conditions are changing dramatically, you should consider making the value of TR a function of dynamic pressure.

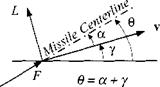
How can we generate the angle of attack from the output of the rate loop? We make use of the incidence-lag relationship. Consider Fig. 9.10 with its lift force L and thrust F. and apply Newton’s second law in the direction normal to the velocity vector v £:

mV у = Fa + qSCRact (9.38)

where we approximated the lift coefficient by its slope CR = CRaoi and assumed

small incidence angles. Taking the time derivative of the angular relationship

а — в — y=q — у (9.39)

and substituting it into Eq. (9.38) yields the incidence-lag differential equation

with the time constant

and the Laplace transfer function of angle of attack wrt pitch-rate response

Ф) _ T

q(s) Tts + 1

The value of the incidence-lag time constant 7} decreases with increasing lift and thrust, reflecting the improved responsiveness of the airframe. For accurate modeling the lift slope coefficient CLa should be made a function of Mach number and possibly of angle of attack.

The airframe block in Fig. 9.9 represents Newton’s equations with the aerody­namic and thrust tables providing the specific forces. Accelerometers, nowadays located in the IMU, measure the accelerations. To keep the simulation simple, higher-order sensor dynamics are neglected.

As an example, I use the acceleration feedback autopilot of the CADAC SRAAM5 simulation. Its position in the logic flow is shown in Fig. 9.11. The guidance module sends the pitch and yaw acceleration commands a^c and au, respectively, to the autopilot, and the measured acceleration [/sp]B comes from the INS. Rocket thrust F is needed for the 7} calculation. The output, incidence angles a and /1, is transmitted to the aerodynamic tables.

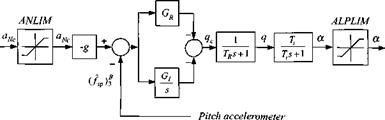
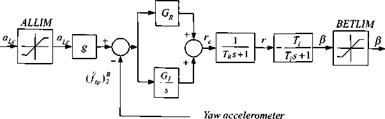
The block diagrams, Figs. 9.12 and 9.13, show in greater detail the actual im­plementation of the pitch and yaw loops. They are very similar, but watch out for the signs (they have been the nemesis of many student projects). We are following the sign conventions of missile aerodynamics. Normal acceleration is positive up and lateral acceleration positive to the right. Pitch rate q, positive up, produces positive a, but yaw rate r, positive to the right, generates negative fi.

Fig. 9.12 Pitch acceleration loop.

The acceleration command, by convention in gs, is converted—after limiting— to the units meters/seconds squared. The error signal is fed through a proportional gain Gr and, for tracking accuracy, through an integrator with gain Gj. After the rate-loop and the incidence-lag transfer functions, the incidence angle is limited before being sent to the aerodynamic tables.

This autopilot must control the vehicle throughout its expansive flight envelope. For air-to-air missiles the excursions are from subsonic launch to triple the sonic speed at motor burnout; incidence angles may reach 50 deg; and the dynamic pressure can change by a factor of 20. Gain scheduling of Gr and G/ provides this flexibility, given the representative time constant TR of the body-rate feedback loop.

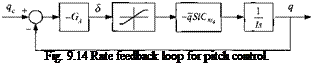
The rate loop transfer function is based on the simplified moment equation about the c. m.

Iq = qSlCms8 (9.43)

with I the moment of inertia, l the moment reference length, 8 the control fin deflection, and Cms the control moment derivative. Figure 9.14 depicts the rate feedback loop for the pitch plane. You should be able to produce the equivalent yaw loop. Ga is the rate loop gain that converts the error signal into a control deflection, followed by the control limiter, the control effectiveness term, and the inertial integrator. The two negative signs are introduced to abide by the aerodynamic convention that a positive control deflection generates a negative pitch rate, but because they cancel, they are of no consequence.

The closed-loop transfer function is of first order with the gain of one and the time constant

Note that the time constant is inversely proportional to the dynamic pressure and the open loop gain GA ■ Its values should be taken from response curves of six-DoF simulations and expressed as a function of q. The CADAC SRAAM5 simulation uses the simple linear relationship Tr = 0.22 — 2 x Q~7 q based on the six-DoF CADAC SRAAM6 data.

I recommend that you use the following root locus technique to calculate the GR and G/ gain scheduling. But first, we have to complete the acceleration feedback loop of Fig. 9.9 by providing the transfer function for the airframe.

Refer back to Eq. (9.38) and recognize that the acceleration normal to the velocity vector is a = Vy. Then, with the definition of the incidence-lag time constant 7) of Eq. (9.41)

and the complete acceleration loop is shown in Fig. 9.15. The open-loop transfer function for the root locus procedure is

Ф) ^ (s + l/TA)

—~7 = IJACP— I v , , ■ (9.46)

£(5-) j(j+ l/7»(s + 1/7-)

with the root locus gain GACp = GRV/(TRTi) and lead time constant TA — Gr/G[. The root locus emanates from the three poles and terminates at the zero and at infinity along two vertical asymptotes.

I picked the gain Gacp = 12.2 with the closed-loop roots —2.7525 + 2.7689/, —2.7525 — 2.7689/, —0.6670 for best performance resulting in GR = 0.0055 and Gi = 0.0046. This type of analysis, applied throughout the flight envelope, gave me the gain schedule Gacp = (0.002q)°-575 and constant TA = 1.2 (see CADAC SRAAM5 simulation).

If the rate loop time constant Tr is not known, a simplified analysis can guide us to select appropriate values. We first develop the transfer function 8(s)/ac(s), then impose the initial value theorem for step input, and finally obtain the relationship

го _ G,GAcpTRTi ^

ac( step) У

The initial fin deflection So, which is also the maximum deflection, is proportional to an acceleration step input aC(step), related by the gains GA and Gacp and the time constants Tr, Tj. Given the maximum control fin deflection and the desired maxi­mum acceleration capability, Eq. (9.47) can be evaluated. However, GA and Gacp are also not known prior to the root locus analysis. Therefore, we have to employ an iterative design technique: Assume a value for TR, conduct the root locus analysis, and verify that the desired acceleration can be achieved. Substituting into Eq. (9.47) the expressions for Tr, Tt, Eqs. (9.44) and (9.41), and solving for ac yields

Note that the dependence on the rate gain GA cancels. Given the maximum control deflection, the achievable acceleration increases with increasing dynamic pressure, thrust, aerodynamic lift slope, and control derivative; and decreases with increas­ing mass properties. A high value of the root locus gain Gacp is also desirable, but must be balanced against the stability requirements.

The acceleration feedback autopilot with inner-rate-loop stabilization finds widespread application in missiles. Its feedback signals are readily obtained from the onboard IMU, and its command signal is directly supplied by the guidance law. On the other hand, angle-of-attack feedback autopilots are also sometimes employed, particularly for high angle-of-attack maneuvers when tight incidence angle control is required. In aircraft angle-of-attack, sensors may be available, but for missiles the feedback signal must be synthesized from IMU measurements and may, therefore, lack accuracy.

Congratulations, you have persevered through the labyrinth of autopilot design for skid-to-tum missiles. But what if you have to model a cruise missile or a bank – to-tum hypersonic vehicle? I will lead you through the steps to modify what you have learned and combine it with a bank-to-tum controller.