Conformal Transformation

3.1 Introduction

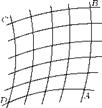
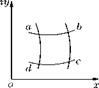
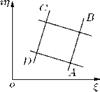
The transformation technique which transforms an orthogonal geometric pattern (Figure 3.1(a)), composed of elements of certain shape, into an entirely different pattern (Figure 3.1(b)), whilst the elements retain their form and proportion is termed conformal transformation.

3.2 Basic Principles

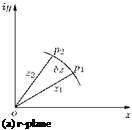
As shown in Figure 3.1, the elements will, in the limit, retain their similar geometrical form. For this to be true, the angle between the intersecting lines in plane 1 must remain the same when the two lines are transformed to plane 2. Let us examine the point p in the (x, iy)-plane (z-plane), referred to as physical plane and the corresponding point P in the (§, in)-plane (f-plane), called transformed plane, shown in Figure 3.2.

In the z-plane (physical plane) point p is located by z = x + iy, and in the f-plane (transformed plane), the corresponding point P is located by f = § + in. The relation between z and f is a particular specified function of f, in terms of z. That is:

This function is known as the transformation function.

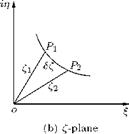
Consider the specific points, located at z1 and z2, on an arc segment p1p2 in the physical plane, as shown in Figure 3.3(a). The corresponding points in the transformed plane are f1 and f2 and the arc segment p1p2 in the z-plane is transformed to curve P1P2, shown in Figure 3.3(b).

For transforming the points in the z-plane to f-plane, the transformation function used is:

f = f (z). (3.1)

Differentiating Equation (3.1), with respect to z, we get:

df = f(z) dz. (3.2)

In the limit of arc length pip2 ^ 0, Sz ^ dz and in the limit of arc length P1P2 ^ 0, Sf ^ df. From Equation (3.2), it is seen that the length df of the segment, in the transformed plane, becomes the vector

Theoretical Aerodynamics, First Edition. Ethirajan Rathakrishnan.

© 2013 John Wiley & Sons Singapore Pte. Ltd. Published 2013 by John Wiley & Sons Singapore Pte. Ltd.

(a) Plane 1 (b) Plane 2

point. dz, in the physical plane, multiplied by the vector f ‘(z), that is:

Now, to understand this operation of the multiplication of vectors, consider the function f (z) rewritten in its exponential form, that is:

f (z) = reli,

where r is the modulus of function f (z). Then:

№1 = ldz|r

Figure 3.3 Transformation of an arc segment.

Figure 3.4 Transformation of crossing arc segments.

is in the direction of dz, after it has been rotated through в, and the angular displacement of f (z) (of the transformed element) is equal to the the length of the original element rotated through angle в and multiplied by r. The shape of the transformed element is given by P1P2, as shown in Figure 3.3(b), and not by Equation (3.2).

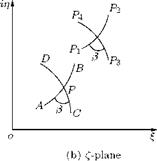
Consider the arc segments ab and cd, cutting each other at point p in the z-plane, as shown in Figure 3.4(a). At point p the angle subtended by the crossing arc ab and cd is в. In the transformed plane (f–plane), in Figure 3.4(b), the corresponding point is P and the transformed curves AB and CD are crossing with the same angle в, in accordance with the conformal transformation, which stipulates that the “angle subtended by two crossing arcs in the physical plane and the angle subtended by the corresponding transformed curves in the transformed plane must be the same.”

Let us consider the actual elements of the crossing arc segments. Since the transformed elements are crossing at point P, with the same angle of intersection as in the z-plane, their lengths would be affected by the same value of the transformation function f (z), in the transformation. Therefore:

P1P2 = p1p2 r, and rotated through в

P3 P4 = p3p4 r, and rotated through в,

where f (z) = re’e.

In the transformation, both the elements of the crossing arc segments are rotated through the same angle. Therefore, the angle of intersection must remain unchanged during the transformation, that is:

Turning angle (в) in the z-plane = Turning angle (в) in the f-plane.

This method can be used to show that a small element abcd in z-plane is transformed to a geometrically similar element ABCD in the f-plane, as shown in Figure 3.5.

This type of transformation satisfies the condition required for conformal transformation. The trans­formation function is essentially of the vector type:

Z = f (z),

where z = x + iy and f = f + iy.

(a) z-plane (b) C-plane

Figure 3.5 Transformation of an element from z-plane to f-plane.

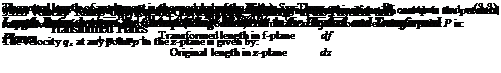A general form of the transformation function is:

At the corresponding points between the original plane (z-plane) and the transformed plane (f-plane), considering only the magnitudes, we can express:

(3.4)

It is seen that the velocity ratio between corresponding points in the original and transformed planes is the inverse of the length ratio.

3.2.3 Singularities

The relation between the corresponding elements in the physical and transformed planes is adequately defined by:

df = f ‘(z)dz.

In most situations, the correspondence between the elements is the modulus and argument of the vector:

f,(z)

as outlined in the previous sections. This arrangement clearly breaks down where f’ (z) = df /dz is zero or infinite. In both the cases, the conformability of the transformation is lost. The points at which df/dz = 0 or <X), in any transformation, are known as singular points, commonly abbreviated as singularities.