Equations of Motion over Round Rotating Earth

Returning to Eq. (9.4), we multiply out the matrices on the left-hand side and express on the right side the aerodynamic/propulsive forces in body coordinates and the gravitational force in geographic coordinates:

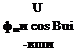= lT]BU^[fa, P]B + [T]UG^[fgf (9.19) ma ma

U is an abbreviation for d/df|i>g|, [T]BU is given by Eq. (9.15), and jT]^0 by Eq. (9.14). These are three first-order nonlinear differential equations with the states U, ij/ui, Oui – Solving for the state derivatives, we discover that in the second equation U cos вщ appears in the denominator. Therefore, these equations cannot be solved if U — 0 or вш = ±90 deg, which we avoid by programming around it. The designation specific force [/sp]B is assigned to the term [fa. P]B/mB, although it has the units of acceleration. (Remember: accelerometers measure specific force.) The gravitational term is simply

= [g]G =

m°

We have succeeded in expressing the equations of motion in matrix form. They are now ready for programming.