Helicopter Systems

6.1 INTRODUCTION

Before discussing the various methods that are employed in the testing of the major systems found in rotorcraft (see Chapter 7) it is necessary to explore the underlying theory and technologies that are involved. This will not only set the testing in context but will help to indicate whether the test techniques themselves are dependent on, or affected by, the actual system under test. In this chapter three major systems are described with which the pilot has an almost continuous interface through routine flight operations: air data systems; engine control and rotor governing systems; and flight control systems (including AFCS). Although the assessment of the mechanical characteristics of powered flight control systems has already been covered technical details of these systems are covered in this chapter for completeness.

6.2 AIR DATA SYSTEMS

6.2.1 Standard atmospheres

The definition of standard atmospheres dates back to the 1920s in the United States and Europe. They were developed in response to a growing need for standardization in aircraft instrumentation and performance measurement. The US atmosphere was developed by the National Advisory Committee on Aeronautics (NACA) [6.1], while the European atmosphere was produced by the International Commission on Aerial Navigation (ICAN) [6.2]. The slight differences between these two independent stand­ards were reconciled and international uniformity achieved by the adoption in 1952 of a new standard. This international standard atmosphere was sponsored by the International Civil Aviation Organization (ICAO) and was defined for altitudes up to 20 km [6.3]. Later work by the US Committee on the Extension of the Standard Atmosphere (COESA), based on data from rockets and satellites, extended this atmosphere to 700 km by 1962 [6.4]. This atmosphere was adopted by ICAO [6.5] as a new standard for altitudes up to 32 km superseding the 1952 ICAO atmosphere.

In 1975 the International Organization for Standardization (ISO) generated a standard atmosphere which covers heights up to 70 km and is based in part on the ICAO standard [6.6]. For heights below 50 km this atmosphere is referred to as the International Standard Atmosphere (ISA), while for heights between 50 km and 70 km it is termed the ‘Interim Standard Atmosphere’. The World Meteorological Organization (WMO) Standard Atmosphere, which is defined between — 2 km and 32 km, is identical to the ISO standard.

6.2.1.1 The atmospheric modelч

The atmospheric model described below has been widely adopted and forms the background to the International Standard Atmosphere. The atmosphere is assumed to consist of a perfect gas with local values of pressure, density and temperature related by the state equation:

P = pRT

The atmosphere is further assumed to be in static equilibrium with respect to the earth such that the following hydrostatic analysis can be made. Consider a small element within the atmosphere of constant cross-sectional area (SA) and height (SZ) centred at some point. Assume that the pressure acting on the base of the cylinder is P and this changes to P + SP at the top. The mass of fluid contained in the cylinder will be equal to the product of its density and volume (p SA SZ) which will generate a downwards force (its weight) equal to mass x the local value of acceleration due to gravity (g). Since the cylinder is in equilibrium:

(P + SP)SA + pg SA SZ – P SZ = 0 SP + pg SZ = 0

Thus:

SZ =-Pg (6Л)

Equation (6.1) provides a relationship between pressure, density and geometric (or tape-line) height. When considering the pressure distribution in the atmosphere it is convenient to use geopotential height (H), which is based on a constant value for the acceleration due to gravity. The geopotential height is the geometric height in a uniform gravitational field that gives the same potential energy as exists at the point under consideration in the actual, variable gravity field. Now the work done in raising a body of mass (m) from one geopotential surface to a higher surface is equal to the potential energy that the body has at the higher surface. If the surfaces are separated by a distance Z then:

g dZ

0

H = —

gsl

This equation relates the geopotential height in a uniform gravitational field, in which the acceleration due to gravity is taken as equal to the sea-level value (gsl), to the actual variation of g with Z. In atmospheric modelling and aircraft performance work gsl is taken as the standard value g0 (9.70665 m/s2) and the resulting measurement of H is called the standard geopotential height. The accepted value of g0 corresponds to a geographic latitude of 45.5425° [6.7].

A relationship between standard geopotential height and pressure can be obtained

by combining the above equations and by assuming that the molecular composition of air is constant over the altitudes of interest. So:

rz

dP P. g0H = g dZ

dZ =-pg = _gRT and Jo

g0 dH = g dZ

Hence:

dP = _ _P_

dH = _g RT

A particular atmospheric model is defined by substituting into Equation (6.2) a given variation of temperature with height and then deducing the corresponding variation of pressure with height. Standard atmospheres consist of layers in which the temperature is either constant or varies linearly with altitude such that:

T = Tb + a(H _ Hb)

where Tb is the temperature at height Hb and a is the temperature gradient, or lapse rate, for heights between Hb and Hb + 1. Thus for the standard atmospheres under consideration, a will either be zero or a constant. Consider a layer where the lapse rate is zero and the temperature is therefore constant at Tb:

lnPb =_Й(H_ Hb)

Now consider a layer where the lapse rate is constant (dT/dH = a) and the pressure is given by Equation (6.2):

dP =_g0 [‘J dT

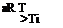P

ln P = _aRln T

Therefore:

PT

PT

6.2.1.2 The International Standard Atmosphere

The first two layers of the International Standard Atmosphere are called the troposphere and the lower stratosphere. In the troposphere, which extends up to 11 km, the temperature falls linearly with a lapse rate of _ 0.0065 K/m (close to 2°/1000 ft) from a sea-level value (T0) of 288.15 K. Above the tropopause, in the lower stratosphere, the air temperature is constant at 216.65 K. With the sea-level ambient pressure (P0) defined at 101 325 N/m2 it is possible to generate specific equations relating pressure to geopotential height. Since most helicopters do not routinely operate above 10 000 ft
(3000 m) we need only consider relationships for the troposphere. Since air at 288.15 K has a gas constant equal to 287.05 J/kg/K and:

P

P T0

P – P (‘+ T0 H

Then substituting for the defined constants into this equation gives the following for H:

P – 101 325(1 – 2.2558 x 10 ~5H)52559 H in metres’)

} (6.3)

P – 101325(1 – 6.8756 x 10 ~6H)5 2559 hin feet J

Note that H can be replaced by Hp (the pressure altitude) as both the sea-level ISA constants and the ISA lapse rate have been used for the formulation of the equations.