Pseudo-Five-DoF Equations of Motion

According to our game plan, the derivation of the equations of motion will pro­ceed from general tensor formulation to specific matrix equations. First, we for­mulate Newton’s second law wrt the flight-path reference frame. Second, we pick either the inertial coordinates ]/ for the round rotating Earth model or the local level coordinates ]L for the flat-Earth simplification. Finally, we develop the kinematic equations that mimic the attitude dynamics.

Attitude information is important even in pseudo-five-DoF simulations. We must calculate the angular velocity u>BI of body В wrt the inertial frame 7 (in six-DoF models шВІ is the output of Euler’s equations) and the direction cosine matrix [Г]®7 of body frame В wrt inertial frame 7. Both are vitally important for the modeling of homing seekers, inertial measuring unit (IMU) sensors, and
coordinate transformations. To construct the body rates, we will use the flight – path-angle rates and the incidence angle rates. Their integrals build the direction cosine matrix.

The key to this venue is the inertial velocity frame U, which is the frame that is associated with the velocity vector v lB of the vehicle’s c. m. В wrt the inertial frame. When Newton’s equations are expressed in this frame, the three state variables become inertial heading angle, inertial flight-path angle, and inertial speed, fljjj, 9ui, vB, with their derivatives dflm/dt, ddui/dt, dv’B/dt. From the first two derivatives we build the angular velocity шиі of the velocity frame wrt the inertial frame. However, to extract the complete body rate u>BI, we need to calculate the angular velocity uiBU of the vehicle wrt the velocity frame. Then we have

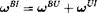(9.1)

Let us pause here and preempt a possible quandary. In Sec. 5.4.2 we derived the pseudo-five-DoF equations for flat Earth and used the velocity frame V of the geographic velocity v f. Now we derive the pseudo-five-DoF equations for a round rotating Earth, still using a velocity frame, but associate it with the inertial velocity v! B. Both velocities are mutually related by Eq. (5.30):

VB = VB + flEIsBi

Therefore, the inertial velocity frame U and geographic velocity frame V are separated by Earth’s angular velocity. Only when we accept Earth as the inertial frame do if and V become the same.

The missing link u)BU of Eq. (9.1) is provided by the incidence angular rates that are computed by the autopilot transfer function. Skid-to-turn missiles use the angle of attack and sideslip angle rates da/dt, df /dt, and bank-to-turn aircraft employ next to the angle of attack also the bank angle rate da/dt, dfrjt/dt.

Before we can express the body rates in matrix form, we must deal with the direction cosine matrix [ T]й/ of vehicle coordinates Iй wrt inertial coordinates ]7. By factoring, we will reach the objective

[■j^j bi [T]BU[T]UI

recognizing that [T]BU is a function of a, f or а, фщ and [T]UI a function of flui, &ui-