Equations of motion relative to the inertial frame

10.1.2.2 In the pre­ceding Hat-Earth approach we had the choice of modeling the equations of mo­tion either in local-level, presumed inertial, or body coordinates. Now we have five possibilities: inertial, Earth, geographic, geodetic, or body coordinates. As bewildering as these choices can be, surveying the literature I find these op­tions: ENDOSIM6 integrates Newton’s equation in inertial coordinates, Euler’s equation in body coordinates and uses quaternions, requiring the introduction of inertial Euler angles. Another U. S. Army simulation7 solves Newton’s equa­tion in geocentric coordinates, while Euler’s equation is again given in body coordinates.

There is little doubt that Euler’s equation should be integrated in body coordi­nates because of the inherent invariance of the MOI tensor. However, for Newton’s equation we have a choice. I prefer the inertial approach, integrating both the ac­celeration and velocity equations in inertial coordinates. The other option is the integration of the geographic acceleration and velocity. We will describe it later. We also have to decide whether we use quaternions or the direction cosine matrix. Because quaternions are closely related to Euler angles, the introduction of inertial Euler angles becomes necessary. I propose that we use the direction cosine matrix and avoid confusing angle definitions.

The derivation of the equations of motion is easy and short. Newton’s law provides

mDlvlB – fa, p +mg

The left side is best expressed in inertial coordinates, but on the right-hand side the forces are formulated in body coordinates and the gravitational acceleration in geocentric coordinates:

m[D4]7 = [T]Br[fa, p]B +m[T]G,[g]G

This leads to the first set of differential equations:

(10.42)

The (T]BI transformation is the direction cosine matrix, and the other transforma­tion [f]GI is obtained from Eqs. (10.36) and (10.39):

Given the inertial velocity [vBY, the inertial displacement vector of the vehicle [яд/]7 is obtained from the second set of differential equations:

= КҐ (10-43)

Equations (10.42) and (10.43) are the translational differential equations, which couple with the rotational equations through the direction cosine matrix [T]BI and the forces [fa, pB ■ A precarious issue is the initialization of the state variables. We will deal with it after we have derived the attitude equation.

The attitude equation is obtained as before from Euler’s law

D’lg = mB

Express the angular momentum as the MOI tensor and the inertial body rates lBg = Ibblobi transform the rotational derivative to the body frame; and finally express the tensors in body axes

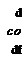5 = + -тв]В) (10.44)

This differential equation is just like the one for the flat-Earth case [Eq. (10.10)], except that the Earth frame E is replaced by the inertial frame I.

Now I must address the initialization of the state variables. So far, we attained nine first-order differential equations, and therefore nine state variables must be initialized. They are divided into three pairs of three each: WBY from Newton’s equation (10.42), [.sg/J’ from the velocity integration Eq. (10.43), and [сошв from Euler’s equation (10.44). The initialization of the direction cosine matrix will be addressed in the next section.

When you build a simulation, you should make it user friendly. Particularly the input should be easy to visualize. Therefore, you want to replace WbY by the geographic velocity vector [uf ]D, expressed in geodetic coordinates. We generate such a relationship by first reviewing the definition of these velocities vB = D1 sBi and vf = DesBe, where sBi — sBe+ sei (E is any fixed point on the Earth and I is Earth’s center), and therefore

D1sBi = DesBe + Desei + EIeisB;

with Desei equals zero because sei is constant in the Earth frame. Thus

VB =VEB+ EIbesBi (10.45)

and expressed in the appropriate coordinate systems

КҐ = [t]D,[vEB]D + (10.46)

Furthermore, because [T]DI is only a function of longitude and latitude, we can summarize: Given the geodetic longitude, latitude, and altitude, and the geographic
velocity vector [i>f ]D, the inertial velocity vector [u^J7 can be initialized. A con­venient alternative to [i>|]D is the initialization by the geographic speed |nf | and the heading angle / and the flight-path angle у, both relative to the local tangent plane. All you need is a conversion routine as, for instance, the CAD AC subroutine MATCAR.

As far as the angular velocity [шві]в is concerned, it is usually initialized by zero values. Only in extreme cases, like close-in air-to-air combat, may the missile have to be given the angular rates of the launch aircraft. Then the aircraft’s initial geographic angular rate [coBE]D has to be converted to the inertial body rate in body coordinates

[шв1]в = [T]BD[coBE]D + [T]BI[coE,}!

where [coEI]! is the Earth’s rotation.

Now, there is an alternate way to initialize the inertial velocity. It is based on Euler and incidence angles. From these angles and the geographic speed the geographic velocity vector can be derived. Express the geographic velocity vector in body and relative wind coordinates ]w

[vE]B = [T]WB[vEB]W = [f]WB

With the transformation matrix Eq. (3.18) introduce the incidence angles

cos a cos /3
sin/6

sin a cos /6

and transform the velocity to geodetic coordinates

[vEB]D = mBD[v ir

The transformation matrix [T]BD contains the Euler angles referred to the geodetic coordinate axes and follows the format of Eq. (3.14). Once [nf ]D is computed, the determination of follows the preceding outline.