Nonlinear Steady Compressible Flow Problem for a Foil

Consider a moderately curved foil in a two-dimensional steady compressible flow near a flat ground. To the lowest order, the corresponding channel flow equation, formulated with respect to the relative motion velocity potential фх, can be derived from the more general three-dimensional equations (5.14)- (5.16) in the form

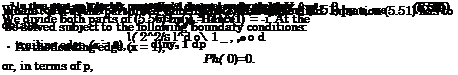1 + ^(7 – 1)M,2(1 – w2) – ^s(*)M02u-jlu2 = 0,

Grouping with respect to d In ys and dp,

(1 + pp){ 1 – p) dlnys – 1(1 + pp)dp + 1m02(1 – p)dp = 0,

Integrating (5.58),

In2/s = ~^ln(l – p)~ ^^-hi(l +pp)+]nC*. (5.59)

Applying the trailing edge condition ys(0) = l, p = 0, we find that С* = 1 so that

4 = (X ~pX1 + PP)M°/>1- (5-60)

Vs

My*)’ where 9 = 9/h, and 9 is pitch. For a flat plate

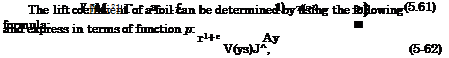
We introduce the pressure coefficient

ys(x) = l + 9x, y’s = e re Є [-1,1],

so that the lift coefficient is given by

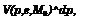
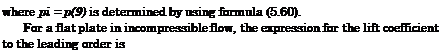(5.63)

Some calculated results, corresponding to the case of a flat plate, are pre­sented versus the relative pitch angle 9 for the Mach numbers M0 = 0.5 and M0 = 0 (incompressible flow case) in Fig. 5.10.