Spinning missile equations

As you stroll through an armament museum and visit the tactical missile section, you will notice missiles with canard or tail control. Tail-controlled missiles, like the Advanced Medium-Range Air-to – Air Missile, have full three axes stabilization and tight control over the three body rates, roll, pitch, and yaw. Canard-controlled missiles on the other hand exhibit a nasty coupling of pitch and yaw control into the rolling moment. Because this rolling moment is difficult to suppress, the airframe is left to roll freely, or, like in the case of the Sidewinder air-to-air missile, the roll rate is dampened by so-called rolerons. A third type of missile is intentionally rolled for stability. A good example
is the Rolling Airframe Missile, which uses angular momentum for gyroscopic stability.

The first type of missile can be modeled by the equations summarized in Fig. 10.1. Spin-stabilized missiles, on the other hand, require a special set of six – DoF equations that decouple the fast roll rate from the pitch and yaw dynamics. A so-called nonspinning reference frame B’ is introduced that slips like a sheath over the spinning body. Its justification comes from the aerodynamic modeling of spinning symmetrical bodies that gives rise to such terms as the Magnus lift and moment coefficients.

The translational equations are transferable from the flat-Earth equations (10.1) and (10.4) by substituting frame B’ for B.

mDB v + mSlB’EvEB = fap + mg with its matrix version expressed in nonspinning body axes ]B

+ m[nB’E]B’[vE f = [fa, p]B’ + m[T]B’L[g]L (10.19)

The ]B coordinates, because they do not follow the rolling of the missile, are obtained from the local-level coordinates by only two rotations, namely, yaw and pitch, thus, the second axis of]5 always lies in the horizontal plane.

The position of the missile follows from the integration of the second set of differential equations (10.4), expressed in ]5 coordinates.

L

= [tfL[vE}B’ (10.20)

These translational equations of spinning missiles have the same appearance as those of nonspinning missiles. The only difference consists in applying the nonspinning reference frame B’ and its associated coordinate system ]5 . Major differences exist, however, in the attitude equations.

The derivation of the attitude equations starts with Eq. (10.7), applied to the nonspinning body frame B’

DB’lBBE + ПВ’Е1ВВЕ = mB (10.21)

We divide the angular velocity шВЕ of the missile body В wrt the reference frame E into two parts:

The first part is the spin rate, and the second part is the angular velocity of the nonspinning shell wrt Earth. Similarly, the angular momentum is split into two parts:

jBE _ jB. .BE _ jB, ,BB’ , jB. ,B’E lB —1ВШ =lBu> +ІВШ

As called for by Eq. (10.21), we apply the rotational derivative wrt to B’

DB'(lBBuBB’) + Db'(Ibbu:b’e) IBBDB’uBB’ +IBBDBшв’Е

where we made use of DB IB = 0, based on the assumption that the missile has rotational symmetry. Thus, the attitude equation of motion is

lBDB’uBB’ + IbDb’u:b’e + Пв’ЕІвшвв’ + ClB’E Івшв’Е = тв

The first term models the change in angular momentum caused by the variable spin rate of the missile. For a missile with constant spin rate, this term is zero. The second term represents the change of angular momentum of the nonspinning body shell as it is subjected to yaw and pitch rate changes. The gyroscopic coupling moment is expressed by the third term, which usually dominates the weaker coupling of the fourth term.

The attitude equation is expressed in nonspinning body coordinates:

Carefully distinguish between the letters В and B’. The point В is always the c. m. of the missile, and the coordinate system is always the nonrotating ]s ; but the frame may be the body fixed frame B, as in /f, or the nonrolling frame B’. as in uB’E.

Rolling missile airframes usually possess rotational symmetry relative to the Is axis. The MOI tensor therefore has a particular simple diagonal form, which is the same in the ]fl and ]fl coordinate systems. With the two cross-principal moments of inertia being equal /3 = /2, we have

0 0 ^"4	B’	CO	B’	V"
0 О	, [coBB’f =	0	, [о/’£]5′ =	я’
О О		0		_r’_

I also included the components of the spin angular velocity [coBB]B and the angular velocity of the nonrolling frame wrt Earth [coDEB. Substituting these matrices into Eq. (10.22) yields

~h{Aco/dt)	B’	ldp’/At	B’	" 0 – r’	я’	B’	~h	0	O"
0	+	hAq’/At	+	r’ 0	-p’		0	h	0
0		hAr’/At		-я’ p’	0		0	0	Z2_

/		B’	r _	B’	r
CO		p’			mBl
	0	+	q’		—	mBl
V	0		r’	)		mB 3_

Matrix multiplications deliver the three scalar differential equations

(dco dp’

71U+dг)=тв>

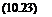h ( + hcor’ – p’r’ih – h) = тв2

h ( – hm’ + p’q’ih – h) = тВз

By definition, the rolling motion of the nonrolling airframe is zero; therefore dp’/dt = p’ = 0, and the equations simplify to

= h l{-h<or’ + mBl) dr’

— = + тВз)

These are the Euler equations for spinning missiles. Compare them with the missile equations (10.16). They differ in the gyroscopic terms. Because of an overriding spin angular velocity со, the gyroscopic moments lcor’ and lcoq’ dominate the cross coupling. The yaw rate r’ couples into the pitch degrees of freedom and, inversely, the pitch rate affects the yaw rate equation. This coupling gives rise to a nutational mode, which effects the missile dynamics profoundly. The programming of these equations follows the same layout as provided in Fig. 10.1, except that the body rates p, q, and r are replaced by the primed variables q’ and r’, while p’ and ф are zero.