Aerodynamics

In the preceding section we concentrated on the left side of Newton’s and Euler’s equations. Now we move over to the right-hand sides and discuss the aerodynamic forces and moments. The modeling of aerodynamics is more of an art than a science because the physics of the airflow over a vehicle is so complicated that even today’s supercomputers have to bow to the supremacy of the wind tunnel. However, the art of modeling aerodynamics is well understood, and we make use of the extensive background material available to us.

Before we proceed, I encourage you to review the five-DoF aerodynamics sec­tion 9.2.1 and the Taylor-series development in Sec. 7.3. For six-DoF modeling the book by Stevens and Lewis9 provides additional up-to-date insight into the linearization process.

Let us revisit the functional dependencies of the aerodynamic forces and mo­ments of Sec. 9.2.1:

aero forces and moments

M, Re, a, p, a, p, p, q, r, 8p, 8q, 8r, c. g., power, shape, scale

^ flow incidence angles body rates control surface

characteristics and rates deflections

where the flow characteristics are determined by Mach number M = velocity/sonic speed and Reynolds number Re = inertia forces/frictional forces. The incidence angles, here in Cartesian form, are the main dependencies. Their derivatives are usually of secondary importance and sometimes combined with the body rates, although their physical origins are quite distinct. The control surfaces are the main moment generators and are crucial for controlled flight. If the vehicle bums much fuel, the c. g. is bound to shift and has to be accounted for. Equally important is the effect of the exhaust plume on the vehicle drag. Hence, power-on/off effects must be included. Finally, the geometric descriptors are shape and scale, but are constant for a given vehicle.

You can imagine there are many techniques to simplify the functional form. The two primary methods are 1) the brute force modeling by tables and 2) the expansion in Taylor series. Diversity arises from the mix of the two approaches. Rather than being all inclusive, I will select three types of vehicles and furnish their aerodynamic models. The FALCON6 represents the aircraft model, NASA’s GHAME6 vehicle exemplifies the hypersonic flight regime, and tactical missiles are embodied by the SRAAM6 concept.

10.2.1.1 Aircraft. Aircraft aerodynamicists, like Lanchester,10 have pione­ered the modeling of aerodynamics. His system of aerodynamic coefficients has served us well over the years. Even rocketeers, after first using ballistic coefficients, have joined up and have used since the early 1960s11 the same framework.

The six-DoF aerodynamic model of an aircraft can be as simple as the linear terms of the Taylor-series expansion or as complicated as tables with five inde­pendent variables. You will find the simple representations in simulations that emphasize autopilot design studies, whereas flight simulators require high-fidelity aerodynamic response for pilot training. We will take the middle road and essen­tially follow Stevens and Lewis.9

Today, the formatting of force coefficients is mostly in body coordinates with the positive sense following the direction of the body axes

[7a?=qS[Cx CY Cz]

where q is the dynamic pressure and 5 the reference area. Gone are the times of using lift and drag coefficients, although we shall encounter this archaic form shortly at the hypersonic vehicle. The format of the moments, referenced to the c. g. B, is noncontroversial and has always been in body coordinates

ImB]B — qS[C/ x b C„, x c C„ x b]

with the reference lengths b as span and c as chord.

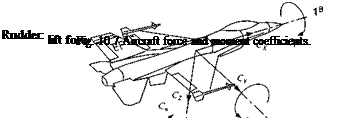
Figure 10.7 should help you visualize the positive directions of the force and moment coefficients. The controls of an aircraft are aileron 8a, elevator 8e, and rud­der 8r. Their positive deflections are defined by the following equations. Whereas a positive aileron deflection causes a positive rolling moment, elevator and rudder deflections are defined as positive if they produce positive increments of lift and side force.

Aileron:

+ALL rolling moment

+<5r -* +ДТ

Now let us expand the aerodynamic force coefficients into a Taylor series but only with respect to the body rates p, q, r and the control deflections aileron, elevator, and rudder, Sa, Se, Sr. The coefficients remain in general a function of Mach M, angle of attack a, and sideslip angle /3. With some variations the following model has been used for the F16 (Ref. 9). Please refer to Eq. (10.61). The axial force coefficient Cx essentially represents drag. Its dependency on Mach number and angle of attack is in tabular form. In addition, the pitch-rate elevator deflection is also tabular because of its nonlinear behavior. Only one Taylor-series expansion term relative to pitch rate is included. It models the drag effect, caused by the increased local angle of attack on the tail, as a result of the pitch rate. Because the side force Су remains usually small, it contains only tables of Mach numbers with the exception of the damping derivatives CYr and CYp, which are also a function of a; otherwise, only the linear terms in the Taylor series of /3, Sa, Sr are taken into account. The normal force coefficient Cz is similar to Cx, except that its dependency on Se can be linearized:

Cx = Cx„(M, a,8e)+^Cx,(M, a)q CY = CYf(M)P + CYJM)Sa + CYJM)Sr

(10.61)

Cz = CZ„{M, a, (3) + CZse(M, a)8e + ^CZq(M, a)q

The rolling and yawing moment coefficients С/ and C„ of Eq. (10.62) are mod­eled in the same fashion with respect to their nonlinear behavior in Their de­pendencies on aileron and rudder deflections have been linearized. In contrast, the
pitching moment Cm is not a function of /3. but the elevator deflection is included in the Cm„ table. An important effect has the center of gravity (c. g.) location on the pitching and yawing moments. Just consider the shift of fuel or cargo during flight. Furthermore, in wind-tunnel testing the moment center of the wind-tunnel model was probably not placed at the c. g. location of the full-up aircraft. In either case, be it dynamic or static, a moment arm xcgR — xcg appears, which couples Cz into C„, and Су into C„. The fixed reference point is at xcgR, whereas the actual c. g is at xcg.

C, = C,„(M, a. P) + QJM, a. P)Sa + Chi (M. a, P)Sr + a)r + Clp(M, a)p

C,„ = a. Se) + ^С,„ч(М, a)q + ^-(xcgR – xcg) (10.62)

C„ — C, h (M, a, P) + C„Sa(M, a. P)Sa + C„Sr(M, a, P)Sr Су b r

– —Ucgr ~ Xcg) + — [C„r(Af, a)r + C„p(M, a)p

Stevens and Lewis9 provide numerical values for the coefficients at the single Mach number of 0.6. You can refer to the aerodynamic tables and mass properties in Appendix A of their book or can go to the CADAC FALCON6 simulation, Module A1.

I had difficulties locating six-DoF aerodynamics of modern aircraft in the open literature. Many of the models are either classified or considered proprietary by the manufacturer. If you have access to flight simulators, ask the software engineer to show you the aerodynamic model. You will be surprised by its sophistication. Here, we are contented with a middle-of-the-road approach.