Altitude hold autopilot

10.2.2.5

10.2.2.6 As mentioned in Sec. 9.2.3.3, there is little difference between an altitude hold autopilot of a pseudo-five-DoF or six-DoF implementation. Refer back to Fig. 9.19 and substitute the acceleration autopilot that we just designed. The altitude and rate measurements are provided by the INS. As before, the root locus analysis will also serve us here and will help us to determine the two gains Gv and Gh – However, I am not building an adaptive gain scheduler as before because altitude corridors are usually fixed, and a constant set of gains will suffice. The hypersonic vehicle GHAME is controlled by this autopilot. You can see the code implementation in the CADAC GHAME6 simulation, Module C2, Subroutine C2ALT.

10.2.2.7 Flight-path-angle controller. Finally, I want to present to you one more autopilot function, the flight-path-angle controller. The aircraft relies on it for climb and descent, especially if the flight-path angle is constrained by air safety rules. You will find this design eminently interesting because it is a perfect example for the pole placement technique of state variables, as embodied by Eqs. (10.77) and (10.78).

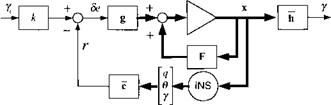
To be specific, we replace the general variable names of Fig. 10.16 with those of our example and present it inFig. 10.19. The commanded and achieved flight path

angle is yc and у, respectively, supplemented by two more state variables: pitch rate q and pitch angle в. All three states are provided by the INS. The three feedback gains c, multiplied by the state vector*, produce the scalar feedback variable r. The elevator deflection be is sent to the actuator. We proceed to calculate the feedback gains c and the feedforward gain k.

First, we copy the plant equation x = Fx + gSe from Eq. (7.73)

with the dimensional derivatives La, L^e, Ma. Mq, M$e. Substituting the plant into Eq. (10.76) yields on both sides third-order polynomials in s, the same order we encountered in the acceleration autopilot. We can, therefore, carry over Eqs. (10.82) and (10.83), but, unfortunately, we cannot solve for the gains by elimination. Instead we have to use Eq. (10.78) and invert the matrix P to calculate the feedback gains:

Once we have c. we proceed to calculate the feedforward gain к from Eq. (10.77). All variables are known, and h = [0 0 1] picks out the state variable y. Using к in the forward loop ensures that the steady-state gain is one, and у will track yc after the transients have died down.

10.2.2.7 Summary. We accumulated a whole assortment of autopilot de­signs for our six-DoF simulations. The rate dampers stabilize missiles off the launch rail and augment the directional stability of aircraft. Roll autopilots are used either to suppress the roll excursions for skid-to-turn missiles or to bank an aircraft into a turn. If this turn leads into a new direction, the heading tracker ensures that the new bearing is maintained. Acceleration autopilots are squarely in the domain of missiles. They execute guidance commands and exploit the full maneuvering capability of the missile airframe. Aircraft are less likely to employ acceleration autopilots, unless they are destined to fly low and hug the terrain while avoiding obstacles. Yet, we embedded an acceleration controller inside an altitude hold loop for air corridor flying. Finally, the climb and descent of an aircraft is controlled by the flight-path-angle controller.

The output of these autopilots are sent to actuators, which rotate control surfaces resulting in moments about the vehicle’s c. m. We will now turn to the dynamic modeling of these actuating devices.