Compensated proportional navigation

Let us briefly review proportional navigation. We choose the guidance law option, which calculates the acceleration command normal to the LOS to the target. Therefore, in Eq. (9.57) the unit vector uv specifically becomes the unit LOS vector mlos

apN = NV£1oiUlos — g (10.100)

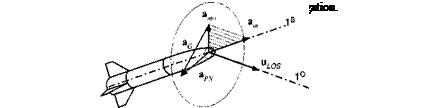
where N is the navigation gain, V the closing speed, $70/ the inertial angular velocity of the LOS wrt the inertial frame, and g the gravity bias. Figure 10.30 shows the vectors that construct this classical guidance law (disregarding g). The guidance command <*pn is normal to the LOS and lies in the so-called LOS plane.

You can visualize the engagement by fixing the target and flying the missile along its Is axis. The LOS rotates with the angular velocity of ш01 in the direction shown, and the vector product with mlos produces the direction of the command ары – Now, if the missile is thrusting and therefore accelerating along its Is axis with am, a parasitic acceleration component appears in the LOS plane that should not contribute to the homing guidance. In effect it introduces intercept errors and should therefore be compensated. If that error is corrected, the PN law receives the prefix “compensated.” We proceed deriving this compensation.

Refer to Fig. 10.31 for the geometric details. The missile’s longitudinal accel­eration am is projected into the LOS plane with the projection tensor PLos

ttmo — Plos rim

and subtracted from the PN command apN to obtain the augmented command

«G = «PN — Ото = «PN “ PLOS = NV n0IU LOS — P LOS^m

If we reintroduce the gravity bias, we have the form of the compensated PN law

aG = NVnOIuLOs – PiosOm ~ g (10.101)

It consists of the basic PN term and the compensation for missile acceleration (or deceleration) and the gravity bias. Notice that I derived it in the invariant tensor form, maintaining its validity in any coordinate system.

To coordinate the law for computer implementation, we proceed in two steps. First, express the guidance command ac in LOS coordinates, then, convert the two components from the LOS plane to body coordinates.

Let us begin with the transformation matrix [T]0B of the LOS coordinates relative to the body coordinates through the azimuth and elevation angles xJ/0B, 9qb, respectively.

‘cos вов cos ir0B cos 90B sin ф0в – sin 90b ‘ – sin іД OB cosmos 0

,sin0oscos іДов sin Bob sin фов cos 90B.

With the missile acceleration vector given in body coordinates [am]B — [am 0 0], the guidance command is expressed in LOS axes (dropping again g for the time being)

[ac]° = [aPN]° – [PLOs]0[T]OB[am]B = [aPN]° –	"0 0 0" 0 1 0	[T]0B	dm 0
	0 0 1		0

Gm

0

-sin if OB sin 9ob COS xj/QB.

Now, we focus on the two components normal to the LOS, which are the com­mands for the autopilot. But because its accelerometers are body mounted, the commands must be converted to body coordinates. Using the (1,1) minor matrix

of Eq. (10.102), we relate the commands

0

cos e0B

and solve for the body coordinates and combine them with the PN and missile accelerations

(ac)f		(apN)f sec – фов + tan іДов
		-(apN)f tan вов tan ф0в + Оры)з° sec вов – ат tan в0в sec іДов_

The component along the missile Is axis was discarded because it contributes nothing to the target intercept.

To sum up, you first calculate the two components of the PN command (apN)^ and (ары)з’ based on the inertial LOS rate received from the seeker. Then, you combine them with the missile acceleration and bring back the gravity bias

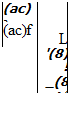(flPK)f sec if OB + dm tan jf0B

-(flpN)f tan вов tan іДов + (арм)° sec Bob ~ am tan 0OB sec ров

(10.103)

You can find this implementation in the CADAC SRAAM6 simulation, Module С1. If you experiment with it, you will find that compensated PN provides some improved intercept performance during close engagements.

Compensated PN plays an essential role in many air-to-air missiles. It converts the inertial LOS rates into acceleration commands and steers the missile into the target. Some recent missile concepts, however, are equipped with strap-down seekers that deliver the target/missile dynamics in Cartesian rather than polar coordinates. For this application, the advanced guidance law, derived from optimal control, is in the right format.