. Error equations for space-stabilized navigators

10.2.4.1 The space – stabilized INS is conceptually the simplest of all navigators because Newton’s

law assumes its most compact form when referred to the inertial frame. The error equations, based on the component perturbations of Chapter 7, form the basis for modeling the navigator of satellites or space ascent vehicles.

Newton’s law states that the inertial acceleration equals the specific force /sp acting on the vehicle plus the gravitational acceleration.

oVB=/sp+* (10.87)

For a space-stabilized navigator we choose the inertial coordinate system, but recognize that the specific forces are most likely measured in coordinates associ ated with the platform or the vehicle’s body.

= {tB,[fsP]B+ [g! (10.88)

The variables in this equation represent the true values, only known by God or the simulation. The values provided by the INS to the guidance processor are the so-called computed variables, which are corrupted by the INS errors. These errors, also called perturbations, are the difference between computed and true values.

Following the methodology of Chapter 7, the component perturbation of any vector x is

ex=x-Rux (10.89)

where x is the computed or corrupted vector and x the true variable. Perturbations of position, velocity, specific force, and gravitational acceleration can be patterned after this equation.

The rotation tensor R11 takes on particular significance. It is the so-called INS tilt tensor that relates the true inertial frame I to the computed frame I. Associated with the two frames are the true inertial coordinate system ]7 and the computed system J/, respectively. All information coming from the INS is expressed in computed coordinates.

Once we introduce these coordinate systems, the component perturbations are reclaimed:

[exl7 = [x]7 – [R7/]7[x]7 = [x]7 – [R11]’^]11 [x]7 and with [Я7/]7′[Г]" = [E]

[ex]7 = [x]7 – [x]7 (10.90)

This equation consists of column matrices, only valid in the chosen coordinate systems. It is not an invariant tensor formulation like Eq. (10.89).

Retracing the development in Sec. 4.1.4, the tilt tensor under small perturbations consists of a unit tensor and a skew-symmetric tensor

[R"]’ = [E]f + [eRn]r

where the perturbation tensor of rotation [see Eq. (4.26)] is expressed by the small

angle components

	‘ 0	—еф	єв~
eR"]1 =	еф	0	—єф
	_ —eO	еф	0

which can be reduced to the tilt vector [r11]1 = [еф єв еф].

This tilt vector represents actually the attitude perturbation, as demonstrated by this simple exercise. Apply the component perturbations Eq. (10.89) to the tilt vector and recognize that the vector product is zero:

ev = r" – RIlr" =r

Indeed, the tilt vector is the tilt perturbation.

The tilt rotation tensor is related to the transformation matrix perturbation by

[ff = [R"]1 = [E]’ + [eR’1]’

and taking the transpose yields the perturbation of the coordinate transformation matrix

[T]" = [E]’ – [eRn]‘

In summary, for the derivation of the error equations I have provided the neces­sary perturbations in Table 10.1. Yet we still need to investigate the time derivative of the velocity vector perturbation. Apply the rotational time derivative wrt the perturbed inertial frame I to the velocity perturbation

D’ev’g = D’v’g – O’ (R"v’g)

The last term is expanded and D’v’B transformed to the / frame to obtain D’v

D'(R"vrB) = D’R"v’B +R” D’v’b = D’R"v’B + R" D’v’g +R"n"v’B

The first and the last term on the right-hand side can be neglected compared to the second term. Owing to the slow Schuler frequency (0.00124 rad/s), the time derivative D1 R" is negligible, and the term R"ft"v’B is small to the second order. With these simplifications Eq. (10.91) becomes

D’ev’g = D’v’g – R" D’v’g

and expressed in ]/ coordinates

The rotational derivatives have become the ordinary time derivatives. With [Rn]1 x [T]u = E] we have a relationship for the perturbed time derivative, which re­sembles Eq. (10.90):

the coupling between the specific force and the tilt, and the gravitational modeling error [eg]7. The specific force error [e/sp]B is a direct result of the accelerometer uncertainties, and the tilt [є/?77]7 is caused by gyro imperfections. From the INS navigation computation comes [T]BI, and [/sp]g is the output of the body-mounted accelerometers. We conclude from the error equation that the INS sensors play a dominant part in the INS quality.

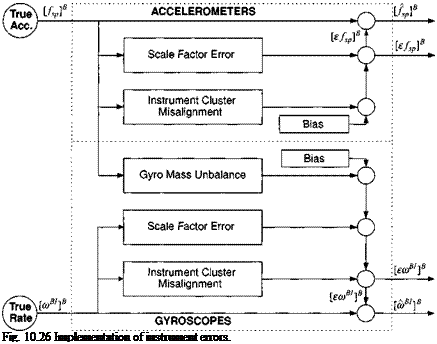
10.2.4.2 Instrument errors. The gyros and accelerometers are either lo­cated on a gimbaled platform or mounted on the vehicle’s body. High-precision navigation systems have platforms—just look at the multimillion dollar INS of the Peacekeeper ICBM. Yet, advances in instrument technology and processing capa­bility have made it possible to replace the gimbals with mathematical models at much lower cost. These devices are called strap-down INS. As already mentioned, our error treatment applies to both; only the numerical values of the parameters reflect the different performance levels. In our discussion, however, we emphasize the strap-down implementation.

A strap-down INS, isolated from structural frequencies by vibration dampers, has two instrument clusters. Its accelerometer cluster consists of three instruments that sense the specific force along the three body axes, and the gyro cluster contains three rotary devices that measure the inertial angular velocity of the vehicle relative to the same three axes.

We model only those errors that remain after factory and prelaunch calibrations have taken place. These primary error sources for accelerometers are random bias and noise, scale factor error and misalignment. The same types of errors apply to gyros, augmented by mass unbalance for mechanical instruments.

The accelerometer error has the form

[e/sp]B = [eba]B + ([Se]B + [Ma]B)[/sp]B

consisting of the random bias and noise [sba]B, the diagonal scale factor error ma­trix [5„] , and the misalignment matrix [Ma]B. The misalignment matrix is skew symmetric, indicating the fact that a small misalignment exists between the ac­celerometer cluster and the vehicle axes. Within the cluster the accelerometer axes are assumed orthogonal. The output of the accelerometer cluster is the measured specific force in body coordinates

[/sp]B = [/s p]B + [£/sp]B

which is a combination of the true value [/sp]B, known only by the simulation and the instrument error [£/sp]B.

The gyro error is composed of similar terms

[sa>B,]B = [sbg]B + ([5,]B + [Mg]B)[a>B,]B + [Ug]B[f%p]B

consisting of the random bias and noise vector [sbg]B7 the diagonal scale factor error matrix [5A,]B, the skew-symmetric misalignment matrix [Mg]B, and addition­ally the diagonal imbalance matrix [UgB, which couples with the specific force. The misalignment again reflects only the cluster error of the otherwise orthogonal gyro triad. The output of the gyro cluster is the measured angular rate in body coordinates

[ftJB/]B = [ft, B/]B + [£WB/]B

composed of the true value [wB/]B and the instrument error [єшв!]в.

The tilt of the INS is caused by the gyro error and grows from some initial value, unless checked by external corrections. An integrator, initialized by the uncertainty of the transfer alignment, models this process:

Г її "l’

d SR“ – R, Dj r,

——- = [T]B,[swBI]B (10.93)

d t

Figure 10.26 summarizes the accelerometer and gyro measurement models. The true states, entering from the left and corrupted by the instrument errors, produce the measured values. Both pairs of output [/sp]B, k/sp]B and [cuB/]B, [ecuB/]B are essential for the INS error model.