Examples of Simple Transformation

The main use of conformal transformation in aerodynamics is to transform a complicated flow field into a simpler one, which is amenable to simpler mathematical treatment. The main problem associated with this transformation is finding the best transformation function (formula) to perform the required operation. Even though a large number of mathematical functions can be envisaged for a specific transfor­mation, in our discussions here, only the well established transformations, which are commonly used in aerodynamics, will be considered. One such transformation, which generates a family of aerofoil shaped curves, along with their associated flow patterns, by applying a certain transformation to consolidate the theory presented in the previous sections, is the Kutta—Joukowski transformation.

Example 4.3

Transform the uniform flow parallel to x-axis of the physical plane, with the transformation function

Z = z2.

Solution

Expressing the transformation function Z = z2, in terms of x and y, we have the following:

Z = z2 = (x + iy)2 = x2 — y2 + 2xiy.

§ + in = X — y2 + i 2xy.

Equating the real and imaginary parts, we get the coordinates § and n, in the transformed plane, as:

22 § = x — y

П = 2xy.

The stream function for uniform flow parallel to x-axis, in the physical plane, is:

f = Vxy.

Therefore:

f

Let f = k.
Vx

Also:

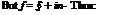
2y

Therefore, § becomes:

t – П 2 § 4y2 y.

Replacing y with k, we get:

§ = — k2

4k2

or:

П = 2k/ § + k2.

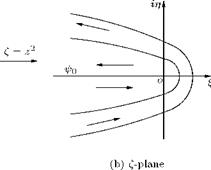
For a constant value of k, this gives a parabola. Therefore, horizontal streamlines, shown in Figure 4.2(a), in the z-plane, transform to parabolas in the f-plane, as shown in Figure 4.2(b). Thus, applying the transformation function f = z2 to an uniform flow parallel to x-axis in the physical plane, we get parabolas in the f-plane.

Note that the flow zones above or below x-axis, in the z-plane, transform to occupy the whole of the f-plane. These zones of the z-plane must be treated separately. In this case, the streamlines in the lower part of the z-plane, extending along the negative y-direction, will be taken with the flow streaming from left to right, in Figure 4.2(b). The streamlines for this flow is given by:

f = Vxy,

where y is always negative. Thus, the stream function is negative in this zone.

Example 4.4

Find the transformation of the uniform flow parallel to the y-axis, in the z-plane, using the transformation function Z = z2.

Solution

The given flow field is as shown in Figure 4.3(a).

For the transformation function Z = z2, from Example 4.3, we have:

22 Z = x – y

П = 2xy.

The stream function for the downward uniform flow, parallel to y-axis, shown in Figure 4.3(a), is:

ф = VyX.

iy■

o

(a) z-plane

Thus, for a given ф and Vy.

ф

x = — = constant. Vy

Let x = — = k.

Vy

The coordinates § and n can be arranged as follows.

П = 2x fxJ-—§.

Replacing x with k, we get.

For different values of k this represents a set of parabolas, as shown in Figure 4.3(b).