. Gravitational error model

The dominant gravitational error is caused by the position error of the vehicle, i. e., the INS processor computes ve­hicle acceleration with an erroneous direction and magnitude of the gravitational vector. For the purposes of this derivation, we consider the gravitational field of a spherical Earth only. Any effects of higher harmonics are of lesser significance. From Newton’s equation of gravitational attraction (see Sec. 8.2.2),

T0000….o derive the gravitational error terms, introduce the perturbations of position and gravitational acceleration from Table 10.1:

/ f GM, f 7.

[g] – [eg]7 = – ………….. , – – ї(Ш’ – [eeB/]7

(кв/1 – Nb/I)3

If the first factor on the right-hand side is expanded into a binomial series

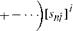
GM – GM / |esB/lT3 / GM

(кв/|-|еев/|)з1%] кв/іЧ кв/І ГВІІ кв/І3

and terms of second order in є are neglected, we obtain

GM GM GM f

[g] – [eg] = ————– ^квЯ + і———- – т[еев/] + 3—— – гкв/] Іеев/І

where the underlined terms are satisfied identically because Newton’s gravitational equation also holds for the perturbed state. The gravitational error equation is then to first-order accuracy

[eg]’ = –—jlssBI]! – з-— квЛ’іеев/І (10.94)

кв/г кв/і

It exhibits the two important elements attributed to the INS navigation error. The first term on the right-hand side conveys the gravitational aberration caused by the location error [е^в/]7, and the second term reflects the error in the distance from the Earth’s center.

All of the elements are now assembled for completing the INS error model. Figure 10.27 depicts the mathematical flow of the equations already derived. First, focus on the three integrators. They represent the three triplets of state variables: velocity error, position error, and tilt. Their initialization is carried out during the transfer alignment of the INS.

The simulation provides the true specific forces and rates, measured and cor­rupted by the accelerometer and gyro triads. After conversion by the tilt transfor­mation, the specific force error is combined with the gravitational error to form the derivative of the velocity error. Like in the actual INS, two integrations lead to the position error. The major outputs of the INS model are the computed values of position [Sgj]1, velocity [t-’g]7, and the direction cosine matrix [T]BI.

You can find this INS error model in the CADAC GHAME6 simulation, Module S4. For a hypersonic vehicle an inertial stabilized INS is quite appropriate. More­over, the simulation builds on a legitimate inertial frame, which is a requirement for this type of model. For other simulations, based on the flat-Earth assumption, we have to proceed in a different fashion.