Heading angle tracker

Heading changes of an aircraft are exe­cuted by roll control. As the lift vector is banked, a horizontal force component generates a lateral acceleration that turns the velocity vector horizontally. Direct sideslip control is ineffective because of the small lateral projected area of the aircraft; also, the ensuing adverse yaw-roll coupling would be undesirable.

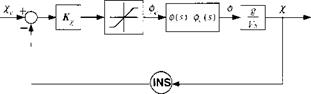We build the heading angle tracker by simply wrapping a heading loop around the roll position autopilot. The schematic is shown in Fig. 10.15. To derive the transfer function from the roll angle ф to the heading angle x, we set up the relationship between the lateral acceleration and the lateral force, caused by the lift vector, banked through the angle </>; and with the small angle assumption of ф, we can

simplify the expression

m Vj( = L sin ф = mg4>

and obtain the desired transfer function

X(s) _ J_

</>(5) Vs

shown in the last block of Fig. 10.15. The gain Kx translates the heading error Xc — X int0 the roll command фс after limits are applied.

We employ again the pole placement technique to calculate this gain. Clinching the open-loop transfer function from Fig. 10.15 and with Eq. (10.74)

t / „ ^ 8

*0S) — Л – V, – у у

fsJ + 2t;consl + co^s

and closing the feedback loop, while setting it equal to the generic third-order transfer function,

T(s) = Kx(8/VH = Kx(g/V)co2n

s3+ 2£wns2 + w2s + Kx(g/V)w2 (s + px)(s2+ 2$xconxs+co2x)

with the free parameters px,£x, and co„x, which determine the modal response of the heading tracker. Equating equal powers of s yields three equations, but, including Kx, there are four unknowns. Hence, one additional equation is required. After having studied the root locus for some time, I found that positioning px on the real axes, directly under the complex poles of the roll autopilot, grants a well – behaved heading response. Thus, we set

Px =

Eliminating and co„x, we calculate the gain from

Kx = -?<o„(l -£2) (10.75)

g

The heading gain depends on the data entry f and con of the roll autopilot and the flight speed V. If the optimal f = 0.707 is selected, the gain is simply Kx = 0.147VoL>n/g. Just as the roll autopilot, the heading loop is also a perfect tracker, thanks to the integrator in the forward loop. You can find the implementation of the heading tracker in the CADAC GHAME6 simulation, Module C2, subroutine C2HEAD. It operates in conjunction with subroutine C2ROLL.