Our heavyweight helicopter equal in the world does not have
In Rostov started production of the most load-lifting rotary-wing car The Russian holding «Helicopt[...]
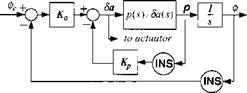
Roll position autopilot
The roll position autopilot has a dual purpose. Missiles, maneuvering independently in the pitch and yaw plane, use the roll autopilot to suppress any roll excursions that may be caused by aerodynamic cross coupling. Although earlier designs, like the Sidewinder air-to-air missile, incorporated only roll damping, all modern missiles possess roll position loops. If the airframe lacks tetragonal symmetry—like cruise missiles or airplanes, the roll loop is used to bank the vehicle for lateral maneuvers.
We build a dual feedback controller, utilizing the roll rate from the INS gyro and roll position from INS navigation computations. The inner rate loop augments the aerodynamic damping and the outer position loop executes the roll command. The transfer function is rather simple, consisting of the roll damping derivative LLp = (qSb/Iu)(b/2V)Cip and roll control derivative LLSa = (qSb/I\)Cis [see Eq. (7.57)]
|
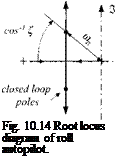
Figure 10.13 depicts the two feedback loops and Fig. 10.14 the associated root locus diagram. The roll autopilot has two gains Кф and Kp that require definition. They give us the added flexibility to specify not only the damping but also the natural frequency of the closed-loop poles. We build first the closed-loop transfer
|
function and set it equal to the desired form that introduces the parameters £ and con:
 |
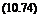
(pis’) KfpLL$a
 |
 |
<pc(s) s2 + (KPLLS„ – LLp)s + КфИца s2+ 2t;(0ns + (О2 Comparing terms of equal power of 5, we can calculate the two gains
The comments I made about rate loops apply here as well. To prevent aileron saturation in extreme flight conditions, you should schedule £ and con and calculate derivatives on-line from stored data. You will be glad to know that, thanks to the integrator in the forward loop, the steady-state error of the roll loop is zero, i. e., the roll position autopilot is a perfect tracker. An implementation of the roll autopilot is given in the CADAC GHAME6 simulation, Module C2, Subroutine C2ROLL.
