Appendix A Matrices

Computer modeling of flight dynamics makes extensive use of matrices. You should already be familiar with the basic concepts of matrix algebra. To refresh your memory, the essential facts are summarized here. For practice you can do the exercises at the end of this section.

A.1 Matrix Definitions

An m x n matrix is a rectangular array of m x n elements arranged in m rows and n columns. For in = 3 and n = 4 we have the 3×4 matrix

3×4	"fill	Й12	Й13	aH~
[A] =	ац	ai2	Й23	aiA
	_г? зі	Й32	ЙЗЗ	Я34.

In general, the subscript notation defines an in x n matrix as

ay, / = 1.2.3….»;: j = 1.2.3….//

The determinant |AI of a matrix [A] is a scalar, obtained from the determinants of the minors My of the matrix [A]:

IAI = (—1)’+-‘cijjMij for; = 1, or2, or3,…, in

The transpose [ B of a matrix [A] is obtained by swapping out the rows and columns [ B] = [A];£>/,■ = ay. A vector is always portrayed as a column matrix. For a 3 x 1 vector

L"3J

The null matrix consists of zero element [0]; 0y = 0; for all / and j. The square matrix has the same number of rows and columns

[A]; a, y,; = 1,…,/?; j = 1,… ,n A matrix is symmetric if it equals its transposed

[A] = [A], cijj = o. y

A matrix is skew symmetric if it equals its negative transposed

[A] = -[A]; cijj = – ay, і ф j; аи = ay = 0, / = j

The skew-symmetric 3×3 matrix is
	■ 0	-аз	a2
[A] =	аз	0	—a
	.-аг	a	0

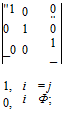	d\	0	0 "
[D] =	0	СІ22	0
	_ 0	0	d33_

The off-diagonal elements of a diagonal matrix are zero. For a 3 x 3 matrix

The unit matrix is a diagonal matrix with unit elements. For a 3 x 3 matrix

The adjoint of a matrix [A] is obtained by adj[A] = transposed of {(— l),+j My}, where My is the minor determinant of ay.

The inverse of a matrix [A] is calculated from its adjoint and determinant: [A]-1 =adj[A]/|A|;|A| * 0.

A matrix [A] is orthogonal if its inverse equals its transposed: [A] 1 = [А]. Other properties are [A][A] = [£]; |A| = ±1.

The rank of a matrix is the largest number r such that at least one rth-order determinant formed from the matrix by deleting rows and/or columns is different from zero. The trace of a matrix is the sum of its diagonal elements.

A matrix [A] can be partitioned into submatrices. For example,

2×1	2×3
Ац	1 to
1×1	1×3
А21	А22

where Ац, Ai2, A2i, and A22 are submatrices.

A.2 Matrix Operations

Two matrices [A] and [В] of dimension m, n are equal if all corresponding elements are equal:

mxn mxn

[ A ] = [ В ], if ay — by, for all i, j

The sum of two matrices [A] and [Л] with the same dimension m, n is obtained by adding corresponding elements:

mxn mxn mxn

[ C ] – [ A ] + [ В ], or су = ay + by, for all i, j

Addition is associative: ([A] + [fi]) + [C] = [A] + ([fi] + [C+]). Addition is commutative: [A] + [Л] = [Л] + [А].

The product of the m x n matrix [A] and the n x r matrix [£] is the m x r matrix [C]:

mxr mxn nxr n

[C] = [A][B]; or ctk = / ajjbjk’, і = 1, • • •, m к = 1, …, r

j=і

where f A] and [fi] must be conformable: m x r = (m x if) {ф x r).

The product of the mxn matrix [A] by the scalar a is

[C]—a[A], or сц = a ay, for all г,;’

Multiplication is associative: [А]([Л][С]) = ([А][Л])[С]. Multiplication is dis­tributive: [А]([Л] + [С]) = [А][Б] + [A][C] but not commutative [A][fi] ф [fi][A], Important rules are the following:

[A][B] = [B][A]

([A][fi])-‘ = [fij-‘tA]-[4], if АфО,ВфО

([А]-1) = ([А]Г1, if АфО Differentiation operates on every element of a matrix [A]: d d

— [A] = —ац, for all і, j and a» must be differentiable dr dr 1 1

Integration operates on every element of a matrix [A]

/

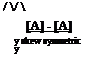Any square matrix [A] can be decomposed as the sum of a symmetric and skew – symmetric matrix:

A.3 Matrix Eigenvalues

The similarity transformation is formed from a square, nonsingular matrix [T] operating on a square matrix [A]:

[А]* = [Г][А][Г]-‘

Two similar matrices [A]* and [A] have the same rank, trace, determinant, and eigenvalues; if [A] is symmetric, so is [A]*. If [Г] is orthogonal, the similarity transformation is [A]* = [T][A][T].

Orthogonal transformations preserve scalar multiplication of vectors, vector addition, multiplication by scalars, absolute values and distances, orthogonality and orthonormality, and value of trace of a matrix. The eigenvalues of an n x n matrix [A] are the roots of the characteristic equation

An n x n matrix has n eigenvalues. A real symmetric matrix has only real eigenval­ues. An orthogonal matrix [Г] has one real eigenvalue ±1 and a pair of conjugate complex poles е±,ф. Given a square matrix [A] with eigenvalues A.,-, then a[A] has the eigenvalues a A,-, and ([A])p has the eigenvalues kf. A square matrix is nonsingular if and only if all its eigenvalues are nonzero.

A matrix [A] can be diagonalized by an orthogonal matrix [Г] if [A] is sym­metric. The determinant of a matrix [A] can be calculated from the product of its eigenvalues IAI = kj.

The trace of a matrix [A] is the sum of all its eigenvalues Tr(A) = Yl’i=і ‘W-

A real, symmetric quadratic form [x][A][x] is symmetric if the matrix [A] is real and symmetric. A real symmetric quadratic form is positive definite, if its eigenvalues are positive.

Problems

A. 1 Partitioned matrices obey matrix operations j ust like regular matrices. Show that the product of two matrices equals the product of their partitioned forms by using the following example:

Г 1	1	11		Г1	2	3	-П
2	-1	0		3	-1	1	0
_-l	0	2_		_0	0	-2	1_

A.2 What is the adjoint and the inverse of matrix [A]?

2 1 3" 4 0-1

3 3 2

A.3 If [A] and [fi] are symmetric matrices of the same dimension, prove that the product [A][fi] is symmetric only if [A][fi] = [Л][А].

A.4 Prove that the square of a skew-symmetric matrix is a symmetric matrix.

A.5 Determine the symmetric and skew-symmetric parts of the matrix [A],

	‘1	2	3"
[A] =	4	5	6
	1	8	9_

A.6 Determine the characteristic equation and the eigenvalues of the matrix [A],

‘2 0 0 ‘

0 3 – y/3

0 – s/b 5