Categories

Special Recent Posts

Our heavyweight helicopter equal in the world does not have

Our heavyweight helicopter equal in the world does not have

In Rostov started production of the most load-lifting rotary-wing car The Russian holding «Helicopt[...]
In Italy broke experimental tiltrotor

In Italy broke experimental tiltrotor

The experimental military man конвертоплан, developed by "August Vestland's" company, brok[...]
The old plane — nonsense, pilots think - there was an attack

The old plane — nonsense, pilots think - there was an attack

In spite of the fact that the main version of crash of the Russian plane of the Kogalymavia company [...]
The Israeli Apache will subject to peeling

The Israeli Apache will subject to peeling

The Israeli shock Boeing AH-64 Apache helicopters will undergo "peeling" procedure. As rep[...]
The aviation industry began to move

The aviation industry began to move

On Monday against Dubai Airshow air show - the 2015th Deputy Prime Minister Dmitry Rogozin blew up t[...]

Closed-Form Integration for H-Force

Posted by admin in Helicopter Performance, Stability, and Control on March 5, 2016

The H – force is the horizontal force perpendicular to the rotor shaft and is derived in the same manner as that of the torque. Figure 3-35 shows the arrangement of the forces on the blades that contribute to the H-forces. At any blade element the incremental H-force is:

AH = f AD – AL — ] sin у — ALB cos у

uT)

In level flight, AH is positive on the advancing side and negative on the retreating side, although in autorotation the reverse can be true. Thus the total H-force can be either positive or negative, depending on which side of the rotor is dominant.

Because of this, the magnitude of the calculated H-force can vary drastically with relatively small changes in flight conditions—or, as will be shown later, with changes in the assumptions made in the integration. When the integration is carried out with the same assumptions as for the thrust and torque equations, the result is:

 

9. + -7-) _ + a0

 

—a,

 

1U { ^0

З Ш 2

 

Again, using the equations for (Bl + al) and (Д — and also the equation for CT/o, the equation simplifies to:

 

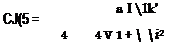i + JL + A^+I _!■_

2 9 2 / 3 CLR 8 CLR

 

4 1 + |T

 

In this case the last term is generally small but perhaps not negligible.

If the inflow portions of the rotor equations are combined, it may be seen

that:

 

£q/Ginflow — ^ CT/0 + a Ct/g)

 

This identity is illustrated graphically by examining the rotor mounted in a wind tunnel at a positive angle of attack, as shown in Figure 3.36. The momentum power that the rotor extracts from the airflow is negative rotor power and is equal

 


Related Posts: