Transformation of Circle to Ellipse

For transforming a circle to an ellipse using the Kutta-Joukowski transformation function:

b2

Z = Z + — z

the circle should have its center at the origin in the z-plane, but the radius of the circle should be greater than the constant b, in the above transformation function, that is, a > b.

With the radius of the circle r = a, we can express the § and n expressions in Equation (4.1) as:

Eliminating в in the § and n expressions above, we get:

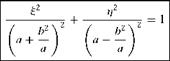(4.3)

This is an ellipse with its major and minor axes, respectively, along the § and n axes in the Z-plane, as shown in Figure 4.5(b).

The major and minor axes of the ellipse, given by Equation (4.3), are The chord or the major axis of the ellipse = Maximum thickness or the minor axis of the ellipse =

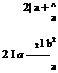The fineness ratio of the ellipse, defined as the ratio of the chord to maximum thickness, becomes:

Chord

Fineness ratio = ————————–

Maximum thickness

b2

a + —

_ _____ a_

= b2

a—-

a

a2 + b2 a2 — b2

or

From this relation it is evident that for every value of the ratio a/b a new ellipse can be obtained.