Transformation of Circle to Symmetrical Aerofoil

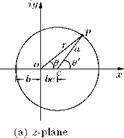
To transform a circle into a symmetrical aerofoil, the center of the circle in the z-plane should be shifted from the origin and located slightly downstream of the origin, on the x-axis, as shown in Figure 4.6(a). This shift would cause asymmetry to the profile (about the ordinates of the transformed plane) of the transformed shape obtained with the Kutta— Joukowski transformation function.

Let the horizontal shift of the center of the circle c, from the origin o, also called as the eccentricity to be e. The actual distance of the center of the circle from the origin is be, as shown in Figure 4.6(a). Thus,

be cos в + a cos у

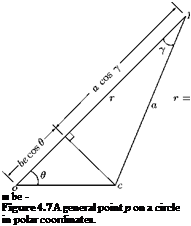the radius of the circle is (b + be). Let us represent the general point p on the circle, in polar coordinates, as shown in Figure 4.7.

The distance of point p from the origin, shown in Figure 4.7, is:

op = r = be cos 9 + a cos у

where e and у are small. Therefore, the above distance r simplifies to:

r = be cos 9 + a

Substituting a = (b + be), we get:

r = be cos 9 + b + be = b(l + e + e cos 9).

This can be arranged as:

b

– = [1 + e (1 + cos 9)]-1. r

But the eccentricity e is very small. Therefore, the term e (1 + cos 9) is very small compared to 1. Thus, expanding the right-hand-side of the above equation and retaining up to the first order terms, we get:

Thus, r and b can be expressed in terms of the horizontal shift e of the circle being transformed.

The transformation function can be expressed, in terms of r and в, by replacing z with re’B, as:

b2

Z = Z + — z

b2

= reie + – e-w

r в + i sin в) + b2 (cos в – i sin в) О о сл r r b r b – +— cos в + ib – — – sin в u r u r

= 2b cos в + i 2be(1 + cos в) sin в.

But:

Z = Z + in

Therefore:

Z + in = 2b cos в + i 2be(1 + cos в) sin в.

Equating the real and imaginary parts, we get the coordinates of the transformed profile as:

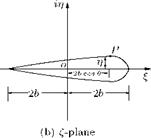
These are the coordinates of a symmetrical aerofoil profile. Plot of Z and n for в from 0 to n and n to 2n gives a symmetrical profile shown in Figure 4.6(b). The chord (the shortest distance from the leading edge to the trailing edge) of the aerofoil is 4b.