Artificial Damping at Surfaces of Discontinuity

A surface of discontinuity such as a wall is a potential source of spurious waves. Thus, it is important to incorporate artificial selective damping near such a surface to suppress the generation of these waves.

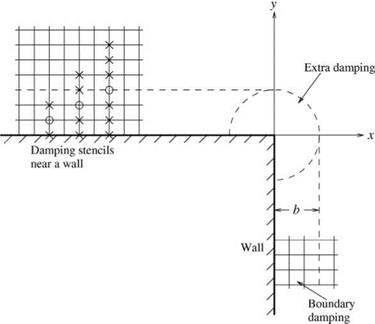
Near a horizontal wall, there is not enough room for a 7-point central damping stencil in the vertical direction for mesh points in the two rows adjacent to the wall (see Figure 7.7). Only a smaller symmetric stencil can fit in the limited space. The following are stencil coefficients for 5-point and 3-point stencils that have been used extensively with satisfactory results.

5-Point Damping Stencil

d0 = 0.375 dx = d—1 = —0.25 d2 = d—2 = 0.0625.

3-Point Damping Stencil

d0 = 0.5

dx = d—1 = —0.25.

The damping curves for these stencils are shown in Figure 7.4. These smaller damping stencils impose a nonnegligible damping on the long waves. They should not be used as general damping stencils over the entire computational domain.

Experience indicates that, when used only near a wall or at the outside boundary of a computational domain, they do not cause excessive damping to the physical solution.

For general background damping, the use of an inverse mesh Reynolds num­ber, Яд1, of 0.05 or slightly less has been found to be satisfactory. The amount of damping is sufficient to remove spurious short waves in most problems. For viscous fluid, additional damping near a wall, especially at a sharp corner (see Figure 7.7), is often necessary. To impose extra damping, a simple but effective way is to use a Gaussian distribution of Яд1 in the direction normal to the wall. The peak value of the Gaussian is at the wall. A good choice of the half-width of the Gaussian is three or four mesh spacings. For instance, along the wall y = 0 in Figure 7.7, an additional inverse mesh Reynolds number distribution of the following form,

Яд1 = 0.15c-(ln2)(H(y), (7.26)

where H(y) is the unit step function, may be incorporated into the artificial selective damping terms of the computation scheme. The highest value of Яд1 at the wall may be larger than 0.1 as indicated above. A similar distribution of inverse mesh Reynolds number distribution may also be imposed adjacent to the wall at x = 0.

At a sharp corner, as shown in Figure 7.7, large amount of artificial selective damping is required to stabilize the computation. This may be implemented by using an inverse mesh Reynolds number distribution at the corner point in the form of a multidimensional Gaussian function,

ЯД = 0.3e~ . (7.27)

At the present time, there are no formal guidelines to setting the amplitude of the Gaussian function at the corner point. This value has to be adjusted in each problem until a satisfactory value is selected.