Climbs and Descents

The closed-form equations can also be used to calculate the power and trim conditions in a climb or in a descent by incorporating the component of gross

TABLE 3.2 Trim Condition Iteration G. W. = 20,000 lb ClR = 650 ft/sec i = .3 (115 kts) p = .002377 (sea-level standard) ax = bx = 0 (This is a valid assumption for performance 1st Iteration analysis, but not 2nd Iteration for stability and control analysis. See Chapter 7) 3rd Iteration dp(start), deg 0 -5.9 -6.1 Lp, lb -200 -730 -746 D„ lb 872 904 904 HM(stztt), lb 181 364 399 Hr(start), lb 12 30 36 T, lb 20,230 20,770 20,790 dppp} nd -.0526 -.0629 —.0647(—3.70°) k’ -.0276 -.0311 -.0316 a0 .0716 .0743 .0744(4.26°) 90, rad .267 .276 .277(15.85°) H*lb 364 399 401 h-p-Af 969 1,089 1,097 TT, lb 677 750 755 Hr, lb 30 36 36 aF, deg -5.9 -6.1 -6.1 A, deg -2.3 В» deg 4.9 h. p.r 25 ®1,270) 4eg 8.3

FIGURE 3.48 Angle of Attack Distribution on Advancing and Retreating Blades

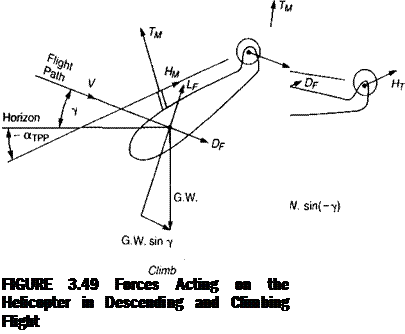
weight that acts along the flight path in the equation for the angle of attack of the tip path plane. Figure 3.49 shows the force balance in a descent and in a climb. The equation for the equilibrium tip path plane angle of attack—using the same derivation as in forward flight—is:

PF + HM + HT + G. W. sin у
G. W. — LF

where

with the rate of climb, R/C, in feet/minute and the forward speed, V, in feet/second. The trim conditions for the example helicopter at 115 knots (|l = .3)

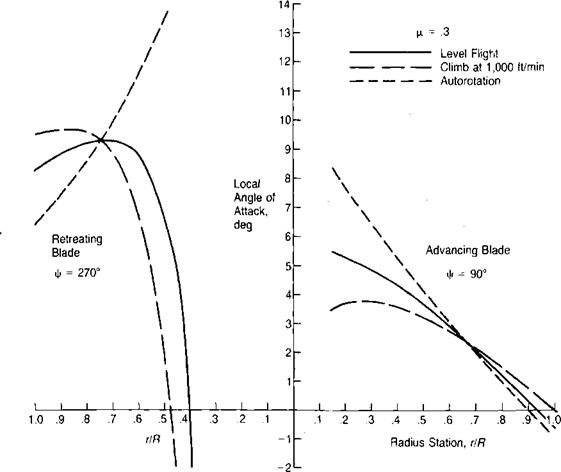
and at a rate of climb of 1,000 feet/minute have been calculated by the same iterative method used for level flight. The results are shown in Table 3.3 and the angle of attack distribution in Figure 3.48.

The difference in power required to climb compared to that required for level flight could have also been roughly estimated from the rate of change of potential energy:

R/C( GW)

33,000

For this case, the estimated difference in power is 606 h. p., whereas the calculated difference (including the tail rotor) is 668 h. p. Thus the example helicopter has a

climb efficiency of 91%. Most of the loss of efficiency can be attributed to the increased fuselage negative lift while a smaller part is associated with the increased tail rotor H-force. This value of efficiency can be used to make rough estimates of the increment in power required to climb at other weights, rates of climb, and speeds in the neighborhood of 115 knots.