Thickness-to-Chord Ratio of the Cambered Aerofoil

Thickness t of the aerofoil at any location along the chord is the difference between the local thicknesses above and below the mid-plane. That is:

t = nu – ni,

where the subscripts u and l, respectively, refer to the upper and lower surfaces of the aerofoil profile. The upper and lower thicknesses of the aerofoil are given, by Equation (4.8ft), as:

Пи = 2be (1 + cos ви) sin ви + 2Ьв sin2 ви П1 = 2be (1 + cos в1) sin в1 + 2bft sin2 в1.

But nu and nl are at the same location on the abscissa (§-axis), therefore, в1 = – ви. The thickness becomes:

t = Пи – Пі

= 4be (1 + cos ви) sin ви.

The thickness-to-chord ratio becomes:

t 4be (1 + cos ви) sin ви

c 4b

or

t <

– = e (1 + cos ви) sin ви.

c

For (t/c)max, the condition is d(t/c)/dв = 0, and d2(t/c)/dв2 < 0. Thus:

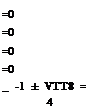d(t/c)/dB e(cos ви + cos2 ви – sin2 ви) cos ви + cos2 ви – (1 – cos2 ви)

2 cos2 ви + cos ви – 1

cos ви

This gives:

cos ви = —1, or 1/2.

We can express this as:

cos ви = -1, at ви = n

and

cos ви = 2, at ви = n/3.

Thus, ви is either n or n/3. At ви = n, t/c = 0, which is the trailing edge of the aerofoil. Hence, t/c should be maximum at ви = n/3.

The thickness-to-chord ratio is maximum at ви = 60°. Thus:

This maximum is also at the quarter chord point, as in the case of symmetrical aerofoil.