J oukowski Hypothesis

Joukowski postulated that “the aerofoil generates sufficient circulation to depress the rear stagnation point from its position, in the absence of circulation, down to the sharp trailing edge.” There is sufficient evidence of a physical nature to justify this hypothesis, and the following brief description of acceleration of an aerofoil from rest may serve as a reminder. Immediately after the state of rest, the streamline pattern around the aerofoil is as shown in Figure 4.13(a).

As seen in Figure 4.13(a), immediately after starting, the rear stagnation point S2 is well ahead of the trailing edge. During the subsequent acceleration to steady motion, the rear stagnation point moves to the trailing edge, a starting vortex or initial eddy is cast off and circulation to an equal, but opposite amount, is induced in the flow around the aerofoil, as shown in Figure 4.13(b).

In the potential flow model of a sharp-edged aerofoil the exact trailing edge point can be defined, because the top and bottom profiles are cusped, at the trailing edge, resulting in zero thickness. It is essential to note that this kind of sharp trailing edge, with zero thickness, is just a mathematical shape,

iy	%n
o	x	o

(a) b = a, center at the origin

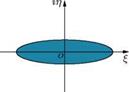(b) b < a, center at the origin

%n
o

(c)

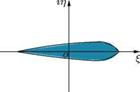b = om < a, center above the origin

(d)

b = om < a, center shifted horizontally

Figure 4.12 Transformation of a circle to (a) flat plate, (b) ellipse, (c) circular arc, (d) symmetrical aerofoil,

(e) cambered aerofoil.

(a)

Figure 4.13 Streamline pattern around an aerofoil (a) just after start, (b) after the starting vortex is established.

and cannot be realized in practice. Actual wing profiles are with a rounded trailing edge of finite thickness. Because of the rounded trailing edge of the wings, in actual flow where viscous boundary layer and wake exist, the position of the rear stagnation point may differ from the location predicted by potential flow theory, and the full Joukowski circulation, may not be established. This is because for realizing full Joukowski circulation, the trailing edge should be of zero thickness and without any wake. This condition of realizing full Joukowski circulation, resulting in flow without wake, is known as Kutta condition.

The Kutta condition is a principle in steady flow fluid dynamics, especially aerodynamics, that is applicable to solid bodies which have sharp corners such as the trailing edges of aerofoils. It is named after the German mathematician and aerodynamicist Martin Wilhelm Kutta.

The Kutta condition can be stated as follows:

"A body with a sharp trailing edge which is moving through a fluid will ‘create about itself a circulation’ of sufficient strength to hold the rear stagnation point at the trailing edge."

In fluid flow around a body with a sharp corner the Kutta condition refers to the flow pattern in which fluid approaches the corner from both directions, meets at the corner and then flows away from the body. None of the fluid flows around the corner remaining attached to the body.

The Kutta condition is significant when using the Kutta—Joukowski theorem to calculate the lift generated by an aerofoil. The value of circulation of the flow around the aerofoil must be that value which would cause the Kutta condition to exist.