Transformation of Circle to Circular Arc

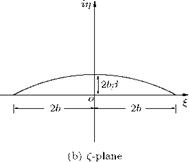
Transformation of a circle with its center shifted above (or below) the origin, on the ordinate in the z-plane, with the transformation function Z = z + b2/z results in a circular arc, as shown in Figure 4.10.

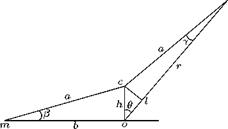
A general point p on the circle with center above the origin, on the у-axis, in Figure 4.10, can be represented as shown in Figure 4.11.

Figure 4.10 Transformation of circle to circular arc.

Figure 4.11 The point p on the circle with its center on the ordinate in the physical plane.

From Figure 4.11, it is seen that:

h = b tan в & Ьв ol = oc cos в = b в cos в lp = a cos у = (b + be) cos у

& b + be (because у is small, cos у & 1).

Therefore,

oP r

r b

or

b -1

– = [1 + (e + в cos в)]

But, (e + в cos в) ^ 1, therefore, expanding the above, retaining only the first-order terms, we get:

b

– = 1 — e — в cos в. r

The Joukowski transformation function is:

b2

Z = z + —.

z

Replacing z = re’e, we have:

ie b2

Z = re’e + —

re

b2

= r(cos в + i sin в) +—— (cos в — i sin в)

r

b2 b2

= r cos в +—— cos в + ir sin в — i— sin в

rr

r b r b

= b —I— cos в + ib [——— sin в.

b+r b r

rb

Substituting for — and -, we get: br

Z = 2b cos в + ib(2e + 2в cos в) sin в ^ + in = 2b cos в + ib(2e + 2в cos в) sin в.

Comparing the real and imaginary parts, we get:

(4.10a)

Equations (4.10a) and (4.10ft), respectively, are the expressions for the abscissa and ordinates of the circular arc, in the transformed plane.

The chord is given by:

§ = (2b cos в) = 4b.

0 0

The camber becomes:

n = n

max

= (2b(e + в cos в) sin в)

= 2be.

But,

be

— = tan в b

e = tan в-

Therefore:

nmax = 2b tan в-

Note: In this analysis, it is essential to note that the angle в, in Figure 4.11, is marked as the angle subtended at the origin o by the line op and the ordinate. This convention is different from that followed in Figure 4.9. This change made is justified by nmax at в = n/2, which has to be satisfied.

4.9.1 Camber of Circular Arc

For the transformed circular arc, the chord is 4b. The camber is the maximum deviation of the arc line from the chord. Thus, the camber-to-chord ratio becomes:

Camber/chord

= – tan в – 2 в

But for small в, tan в ^ в. Therefore, the percentage camber for the circular arc becomes 100 в/2.

b2

Thus, on transformation with Z = z +—— , a circle with its origin on the y-axis, as shown in Figure

z

4.10(a), transforms to a circular arc of camber-to-chord ratio в. This is the extreme case of Joukowski profile, for which the camber is finite and the thickness is zero.

The transformation of a circle of radius a in the z-plane with its (a) center at the origin and b = a, (b) center at the origin and b < a, (c) center above the origin and b = om < a, (d) center shifted horizontally and b = om < a and (e) center in the first quadrant and b = om < a, using the Joukowski transformation, Z = z + b2/z, results in a flat plate, ellipse, circular arc, symmetrical aerofoil and cambered aerofoil, respectively, as shown in Figures 4.12(a)-4.12(e).