Steady-state flight and trim conditions

It is important to obtain steady-state flight conditions for obtaining the linearized mathematical models of the aircraft at various flight conditions, since these models are required for the design of control laws [2,9,13]. An aircraft is considered to be in

an equilibrium state when all its state derivatives become zero simultaneously, the mass being assumed constant. This is a stringent requirement and it may not be possible to attain this in all types of flight conditions. The conditions like wings-level and level turn, wherein the rotational and translational accelerations are zero and with Euler angular rates as constants, are practically feasible situations and hence useful to study. Such conditions are called quasi-steady states. To obtain steady-state equilibrium of aircraft (dynamics), the trim state should be obtained by estimating the control settings such that the accelerations have zero values. The equilibrium point is f (x, x, u) = 0, with x = 0, u = 0, or constant. Due to this condition the system is at rest. The aircraft then flies in steady wings-level and can have steady turning flight. Also, a wings-level climb and a climbing turn are possible. The steady flight is defined in terms of the following variables: p, q, r, V, a, 3 = 0; u = constant.

Flight-specific constraints are

Steady wings-level: f, f, U, ф = 0 (p, q, r = 0);

Steady turning : U, f = 0 (turn rate ф)

Steady pullup : f, f, ф = 0 (pullup rate (?)

Steady roll : U, ф = 0 (roll rate f)

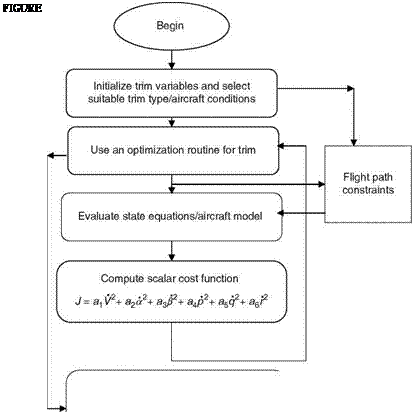
The condition p, q, r = 0 dictates that the angular rates and aerodynamic and thrust moments should be zero or constant. Also, V, a, 3 = 0 dictates that the aerodynamic forces should be zero or constant. In order to arrive at steady-state conditions, a set of nonlinear simultaneous equations need to be solved. Due to the complexity of the EOMs, a numerical routine is necessary to adjust the independent variables to meet required criteria/constraints. The knowledge of aircraft behavior would be useful to specify steady-state conditions and achieve the required trim. A trim routine flow diagram is given in Figure 6.6. For steady translational flight, the constraints are p, q, r, f = 0. The trim surface positions and other variables are determined by numerically solving the nonlinear equations for translational and rotational acceler­ations. The pitch attitude can be determined from the attitude rate.

For pullup/pushover the trim is computed with the following conditions: p, r, f = 0. The pitch rate is computed as:

q = {mg(n + cos(a — ()) — ZT cos a + XT sin a} (6.13)

Vm cos 3

There are other trim conditions possible: (1) thrust-stabilized turn trim, (2) specific power trim, and (3) 3 trim. The thrust-stabilized condition yields a constant nonwings-level turn with a nonzero altitude rate. The constraints are the same as the level turn. The altitude and the Mach number are specified for the thrust – stabilized trim condition. The specific power trim situation yields a level turn at specified altitude, thrust trim parameter, specific power, and the Mach number. The specific (excess) power is given by (see Exercise 7.9)

dh V dV d t g d t

Then the velocity rate is obtained, with the altitude kept constant:

V = pf (6.15)

The other states p, q, r, a, /3 would be zero if the required trim point is obtained. Other constraints need to be satisfied for this specific power trim [14].

Example 6.1

Develop trim routine based on MATLAB following the flow diagram given in Figure 6.6. Aircraft geometry/configuration data need to be provided for the chosen aircraft. Also aerodynamic derivatives (or the aero database/aerodynamic coefficients are needed [2]). This builds up the math model of the aircraft. The cost function needs to

TABLE 6.2 Results of Aircraft Trim Routine Altitude Airspeed Cost Throttle Elevator Alpha (ft) (ft/s) (Approximate) Value (°) (°) 0 150 2.0e-25 0.254 — 18.2 22.8 20k 300 2.02-24 0.176 4.29 8.88

be tailored to specific aircraft/sets of equations. MATLAB’s “fminsearch” can be used for minimization of the chosen cost function.

Solution

The programs (for a transport aircraft/for three degrees of freedom (3DOF) model) written in MATLAB are given in the directory ‘‘ExampSolSW/Example 6.1Trim.’’ The file ‘‘main. m’’ needs to be run in MATLAB. You can specify speed and altitude. Some results are given in Table 6.2.