The Exact Joukowski Transformation Process and Its Numerical Solution

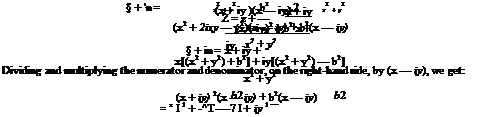The coordinates of the transformed aerofoil profile are obtained as follows. The transformation function can be expressed:

Comparing the real and imaginary parts, we get the coordinates of the aerofoil sections as:

b2

b2

x2 + y2

Referring to Figures 4.8 and 4.9, we have the distance op of point p from the origin in the z-plane, as:

op = r = be cos в + h sin в + a cos y.

The x and y coordinates of point p are:

x = a cos в’ + be y = a sin в’ + bp (1 + e).

With a = (b + be), the above coordinate expressions become:

x = (b + be) cos в’ + be, (4.16a)

y = (b + be) sin в’ + be(1 + e).

where e and в represent the thickness and camber of a given aerofoil, respectively. Therefore, the values of x and y can be found for the given values of 9′, round the circle, from 0 to 2n. Substituting these x and y in to Equations (4.15a) and (4.157), the aerofoil coordinates § and n can be obtained.

This method may be used with both singularities within the circle, when:

x = a cos 9′ + be a = b (1 + e) e « 1.