Flight Simulation Model Validation Using Direct Update

Another approach based on parameter-estimation technique that allows direct updates to the aerodynamic coefficient is briefly discussed [20]. It has the merits of capturing the nonlinearities in coefficients, joint dependence of a particular coeffi­cient on one or more independent variables, like a, b, d, and Mach number, and can encompass a process of model structure determination using splines and modified regression methods. The wind-tunnel predictions using the method of incremental coefficients determined from the flight data have been studied in Refs. [21,22]. In the present approach the nonlinear aerodynamic functions are obtained in the table lookup form. First, a nonlinear short period model to account for nonlinearities is postulated:

(6.32)

The functional dependency on more than one variable can also be considered:

(6.33)

To represent a nonlinear term (say, between two breakpoints) the interpolation formula can be used for the pitching moment as

Here, the nonlinear function is expressed in the form of a linear combination of the weights and the components of the moment variable at the breakpoints. Similarly, the expressions for 2-D formulae to represent the dependent variable as a function of two variables can be obtained:

M(a, b) = Wn (a)Wt2(b)Mij + Wa (a)Wr2(b)MiJ+1 + Wri(a)Wa(b)Mi+ij

+ Wr1(a)Wr2(b)Mi+1J+1

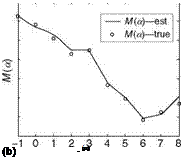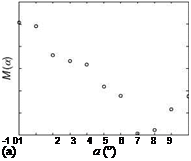
FIGURE 6.12 Aero data base validation: comparisons using direct method. (a) Estimate from flight data and (b) estimate compared with true value.

With a 2 [a,-, ai+1] and b 2 b,,bi+1]. The weights can be computed separately for each dimension as done for the 1-D equation. Moment-related dependent variables are unknowns. The nonlinear functions M(a), Z(a) are estimated treating them as the function values at selected breakpoints expressed in the form of the following equation:

The above equation can be written in short as Y=Xb, with b as the parameter matrix, which is estimated using LS method: b = (XTX)^1XTY. Figure 6.12a shows a typical result obtained from the flight data of a supersonic fighter aircraft and Figure 6.12b shows the validation of the concept. The procedure is versatile and it should be validated using various flight databases.