The empennage aerodynamic forces and moments
The horizontal tailplane and vertical fin, together forming the empennage of a helicopter, perform two principal functions. In steady forward flight, the horizontal tailplane generates a trim load that reduces the main rotor fore-aft flapping; similarly, the vertical fin generates a sideforce and yawing moment serving to reduce the tail rotor thrust requirement. In manoeuvres, the tail surfaces provide pitch and yaw damping and stiffness and enhance the pitch and directional stability. As with the fuselage, the force and moments can be expressed in terms of coefficients that are functions of incidence and sideslip angles. Referring to the physical layout in Fig. 3.32, we note that the principal components are the tailplane normal force, denoted Ztp, and given by
1 2
Ztp = 2pVtpStpCztp(atp, Ptp) (3.252)
which gives rise to a pitching moment at the centre of gravity, i. e.,
Mtp = (ltp + xcg) Ztp (3.p53)
and the fin sideforce, denoted by Yfn, i. e.,
1 2
Yfn = pPVfrSfnCyjn(afn, f) (3.254)
which gives rise to a yawing moment at the centre of gravity, i. e.,
![]()
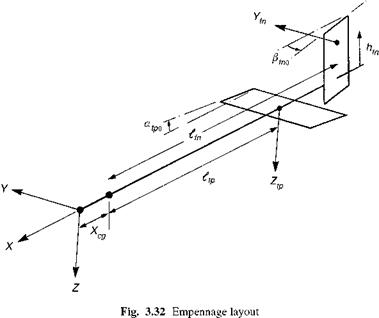 |
Nfn — (lfn + xcg) Yfn
where Stp and Sfn are the tailplane and fin areas respectively.
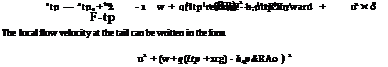 |
|
The local incidence at the tailplane, assumed constant across its span, may be written as
where
![]() (3.259)
(3.259)
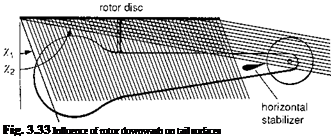
The parameter kxtp defines the amplification of the main rotor wake uniform velocity from the rotor disc to the tail. The tailplane incidence setting is denoted by atp0. The main rotor wake will impinge on the horizontal tail surface only when the wake angle falls between X1 and X2, given by (see Fig. 3.33)
otherwise, kxtp can be set to zero.
In Ref. 3.49, Loftin gives wind tunnel measurements for a NACA 0012 aerofoil section for the complete range of incidence, -180° < a < 180°. From these data, an approximation to the normal force coefficient can be derived in the form
Cztp < Cztpl Cztp (atp) — a0tp sin atp (3.261)
і і sin atp
|QJ > Czp Czp(atp) — – Czp у—p (3-262)
 |
where a0p is, effectively, the slope of the tailplane lift coefficient curve for small angles of incidence. The value of this parameter is assumed to be a mean value for the whole surface. Typically, helicopter tailplanes are fairly low aspect ratio surfaces, sometimes having endplates to increase the effective angle of attack. Values of a0tp between 3.5
and 4.5 are typical. The constant limit value Cztpi is approximately 2 for the NACA 0012 aerofoil, corresponding to the drag coefficient in two-dimensional vertical flow.
The above formulation, leading to constant rotor downwash over the tailplane, can be improved in two relatively simple respects. First, the spanwise variation of downwash at the tail can be derived from the lateral distribution of downwash from the main rotor, Лі. Second, the downwash at time t at the tail can be estimated from the loading conditions at time t — St on the main rotor, where St is the time taken for the flow to reach the tail. This effect manifests itself in an acceleration derivative, or force and moment due to rate of change of incidence, and is discussed in more detail in Chapter 4. The lateral variation in downwash over the horizontal tail generates a roll moment and can also lead to a strong variation of pitching moment with sideslip, as discussed by Cooper (Ref. 3.50) and Curtiss and McKillip (Ref. 3.51).
The local angle of sideslip and velocity (in x-y plane) at the vertical fin may be written in the form
The loading on the vertical surface can be derived in much the same way as the tailplane, either as a simple analytic function or via a table look-up. One additional complexity, characteristic of helicopter fins, is that they are sometimes quite thick aerofoil sections, carrying within them the tail rotor torque tube. The lift generated at small values of incidence on aerofoils with thickness ratios greater than about 20% can be negated by the lower surface suction near the trailing edge, as discussed by Hoerner and Borst (Ref. 3.52). Figure 3.34, approximated from wind tunnel measurements on the SA 330 Puma (Ref. 3.53), shows how the fin sideforce varies with sideslip angle; over the first 5° of incidence, no lift (sideforce) is produced. This effect partly explains the loss of directional stability and attendant weak Dutch roll damping on the Puma, an aspect that will be the subject of further discussion in Chapters 4 and 5.
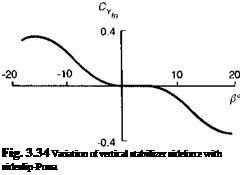 |
The forces generated by the empennage at small values of incidence and sideslip can be represented either by look-up tables or by high-order polynomials, e. g., the Puma
fin sideforce requires at least a fifth-order function to match the strongly nonlinear feature illustrated in Fig. 3.34 (see the Appendix, Section 4B.1).











