Our heavyweight helicopter equal in the world does not have
In Rostov started production of the most load-lifting rotary-wing car The Russian holding «Helicopt[...]
The General Case
In using cylindrical coordinates for two – or three-dimensional computation, there are two basic problems in computing the solution at and near r = 0. The first problem is how to approximate d/dr by a finite difference quotient at mesh points close to r = 0. The second problem is how to calculate the solution at r = 0 where there is an apparent singularity. This section addresses these two issues in the general situation.
9.4.2.1 Directional Derivative
Let es be a unit vector in the і direction as shown in Figure 9.5. To approximate З/Зі, one may use a 7-point finite difference quotient on a line in the es direction as shown; i. e., 1
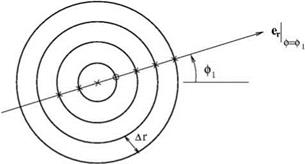
Figure 9.6. Approximating the r derivative at ф = ф1, r = Ar as directional derivative by a 7-point stencil finite difference quotient.
Here, ЭФ/Эз = es – VФ is the directional derivative of Ф in the es direction. j = 0 is the point at which the derivative is to be computed.
9.4.2.2 r Derivative of a Scalar Variable Near r = 0
 |
 |
 |
The r derivative of a variable Ф at ф = фх and r = Ar (see Figure 9.6) may be regarded as a directional derivative. That is,
 |
A finite difference approximation to the directional derivative of Eq. (9.31) may be formed in the same way as Eq. (9.30). Thus,
where the origin r = 0 is at j = -1. In this way, except for r = 0, there is no problem in computing the solution to the discretized Navier-Stokes equations on a cylindrical coordinate mesh.
9.4.2.3 Scalar Variables at r = 0
Because the Navier-Stokes equations in cylindrical coordinates have apparent singularities at r = 0, the values of scalar flow variables cannot be advanced in time by means of the discretized form of the equations. To find the values of the scalar variables at r = 0, a simple way is to compute first the solution at all other mesh points in the computational domain. After this is done, the values of the flow variables at r = 0 may be found by using high-order multidimensional optimized interpolation based on the values of all the mesh points on the first three rings of the cylindrical mesh. Just an average of all the values of the variable on the first ring is often a good approximation. For this purpose, the multidimensional optimized interpolation method of Chapter 13 would be very useful.
